Question

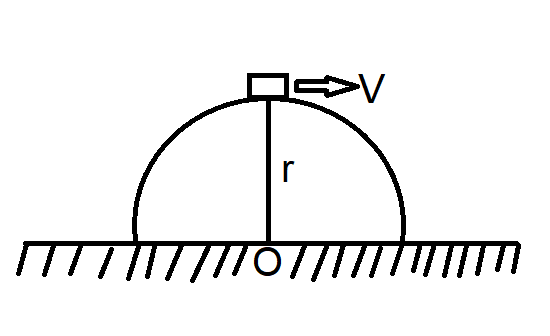
Find its position at the instant it leaves the hemisphere

A. r/4
B. r/2
C. r
D. 2r/3

Answer 1

Hint: It is advised to make the free body diagram while solving this question. Key point to keep in mind while solving this question would be that the normal force disappears when the body is about to leave the hemisphere, meaning N = 0. Also, the force on the hemisphere would be equal to the centripetal force at that instant.

Complete answer:
Before we start solving the question that has been given to us, let us take a look at all the parameters that have been given
Mass of the block = m
Let the position be at height h form the floor so,
Height = h
Radius = r
Now we will have the free body diagram,

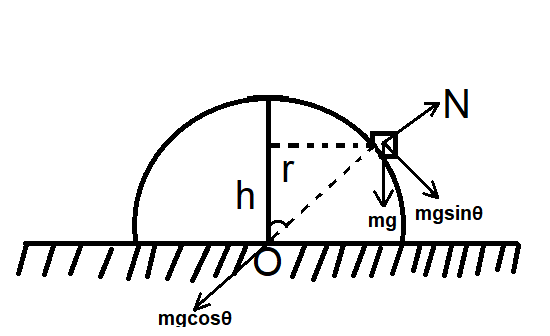
Now,
\[Fc=mgcos\theta -N\]
When the body leaves the hemisphere, the normal force will become zero
So,
N = 0
\[{{F}_{c}}=mg\cos \theta \] …………….. (1)
Also,
\[{{F}_{c}}=\dfrac{m{{v}^{2}}}{r}\] ……………….. (2)
So, now we have
\[\Rightarrow mg\cos \theta =\dfrac{m{{v}^{2}}}{r}\]
\[\Rightarrow g\cos \theta =\dfrac{{{v}^{2}}}{r}\]
\[\Rightarrow {{v}^{2}}=gr\cos \theta \]
As we know
$\cos \theta =\dfrac{h}{r}$
So,
\[{{v}^{2}}=gh\]
\[\Rightarrow v=\sqrt{gh}\]
Now,
Now, from conservation of energy
\[{{U}_{i}}+{{K}_{i}}={{U}_{f}}+{{K}_{f}}\]
So,
$\Rightarrow mgr+0=mgh+\dfrac{1}{2}m{{v}^{2}}$
$\Rightarrow gr=gh+\dfrac{1}{2}{{v}^{2}}$
But,
\[{{v}^{2}}=gh\]
So,
 $\Rightarrow gr=gh+\dfrac{1}{2}gh$
$\Rightarrow gr=\dfrac{3}{2}gh$
$\Rightarrow r=\dfrac{3}{2}h$
Therefore,
$\Rightarrow h=\dfrac{2}{3}r$
So, the position at the block at the instant it leaves the hemisphere will be
$h=\dfrac{2}{3}r$

Note:
In the answer the height is measured from the bottom of the hemisphere or floor. Meaning, the position of the block at the instant it leaves the hemisphere will be at a distance $\dfrac{2}{3}r$ form the bottom or floor.