
Find intervals for which f is increasing and decreasing, local max and local min, concavity and inflection points?
\[f\left( x \right) = \sin x + \cos x,\left[ {0,2\pi } \right]\]
Answer
480.3k+ views
Hint: In the above given problem, we are given a trigonometric function which is the sum of two trigonometric functions, the sine and cosine functions. The interval of this function is given as \[\left[ {0,2\pi } \right]\] . We have to find the intervals in which f is increasing and decreasing, the local maxima and local minima, its concavity and the inflection points for the given function. We can approach the required solutions by using the first and second derivative methods.
Complete answer:
Given trigonometric function is \[f\left( x \right) = \sin x + \cos x\] .
The interval of this function is given as \[\left[ {0,2\pi } \right]\] .
We have to find the increasing and decreasing intervals of this function along with the local minima and maxima, concavity and inflection points.
We can approach them using the method of first and second derivative tests.
Since the function is,
\[ \Rightarrow f\left( x \right) = \sin x + \cos x\]
Hence, differentiating the function once gives us,
\[ \Rightarrow f'\left( x \right) = \cos x - \sin x\]
For the inflection points of a function, we have \[f'\left( x \right) = 0\] , that gives us the equation as
\[ \Rightarrow f'\left( x \right) = \cos x - \sin x = 0\]
Hence,
\[ \Rightarrow \cos x = \sin x\]
That gives us two values in the interval which satisfy the above condition,
\[ \Rightarrow x = \dfrac{\pi }{4},\dfrac{{5\pi }}{4} \in \left[ {0,2\pi } \right]\]
These are the critical points.
Now, the second derivative of the function is given by,
\[ \Rightarrow f''\left( x \right) = - \left( {\sin x + \cos x} \right)\]
Now, at \[x = \dfrac{\pi }{4}\] we have,
\[ \Rightarrow f''\left( x \right) = - 1 < 0\]
Hence it has local maxima at \[x = \dfrac{\pi }{4}\] .
That is,
\[ \Rightarrow f\left( {\dfrac{\pi }{4}} \right) = \sin \left( {\dfrac{\pi }{4}} \right) + \cos \left( {\dfrac{\pi }{4}} \right) = 1\]
Also, at \[x = \dfrac{{5\pi }}{4}\] , we have
\[ \Rightarrow f''\left( x \right) = 1 > 0\]
Hence it has local minima at \[x = \dfrac{{5\pi }}{4}\] .
That is,
\[ \Rightarrow f\left( {\dfrac{{5\pi }}{4}} \right) = \sin \left( {\dfrac{{5\pi }}{4}} \right) + \cos \left( {\dfrac{{5\pi }}{4}} \right) = - 1\]
Now, we have to check the nature of the function after \[0,\dfrac{\pi }{4},\dfrac{{5\pi }}{4}\] .
The sign chart for the function \[f\left( x \right) = \sin x + \cos x\] can be shown as:
Now for the concavity of \[f\left( x \right) = \sin x + \cos x\] , we have \[f''\left( x \right) = 0\] , that gives us
That gives,
\[ \Rightarrow \sin x = - \cos x\]
The values which satisfy above condition are,
\[ \Rightarrow x = \dfrac{{3\pi }}{4},\dfrac{{7\pi }}{4}\]
These are the inflection points.
Again, the sign chart for the concavity of the function \[f\left( x \right) = \sin x + \cos x\] can be shown as:
Note: We can also draw the graph of the function \[f\left( x \right) = \sin x + \cos x\] which shows the concavity and as well as the increasing decreasing nature of the given trigonometric function.
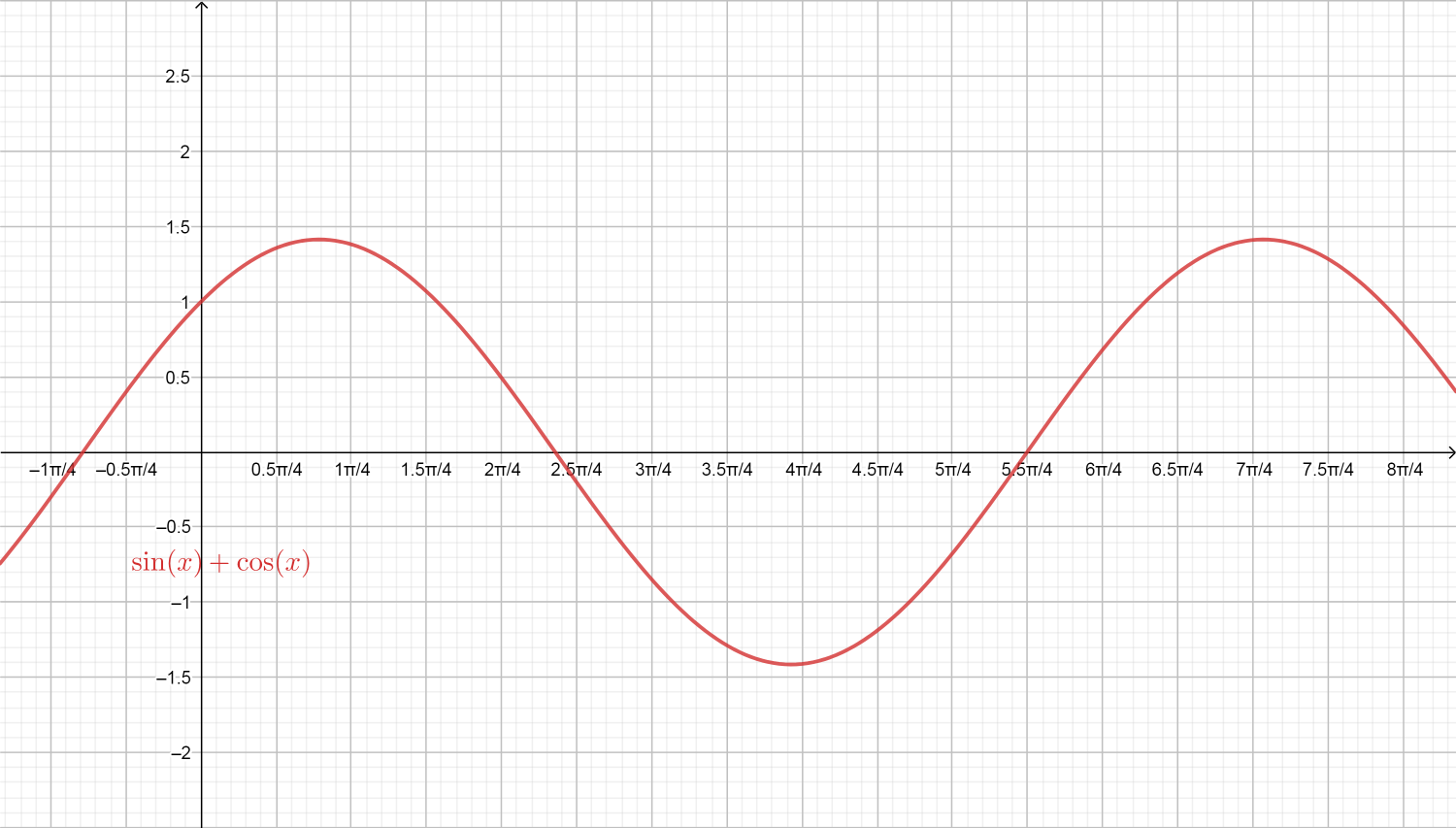
Complete answer:
Given trigonometric function is \[f\left( x \right) = \sin x + \cos x\] .
The interval of this function is given as \[\left[ {0,2\pi } \right]\] .
We have to find the increasing and decreasing intervals of this function along with the local minima and maxima, concavity and inflection points.
We can approach them using the method of first and second derivative tests.
Since the function is,
\[ \Rightarrow f\left( x \right) = \sin x + \cos x\]
Hence, differentiating the function once gives us,
\[ \Rightarrow f'\left( x \right) = \cos x - \sin x\]
For the inflection points of a function, we have \[f'\left( x \right) = 0\] , that gives us the equation as
\[ \Rightarrow f'\left( x \right) = \cos x - \sin x = 0\]
Hence,
\[ \Rightarrow \cos x = \sin x\]
That gives us two values in the interval which satisfy the above condition,
\[ \Rightarrow x = \dfrac{\pi }{4},\dfrac{{5\pi }}{4} \in \left[ {0,2\pi } \right]\]
These are the critical points.
Now, the second derivative of the function is given by,
\[ \Rightarrow f''\left( x \right) = - \left( {\sin x + \cos x} \right)\]
Now, at \[x = \dfrac{\pi }{4}\] we have,
\[ \Rightarrow f''\left( x \right) = - 1 < 0\]
Hence it has local maxima at \[x = \dfrac{\pi }{4}\] .
That is,
\[ \Rightarrow f\left( {\dfrac{\pi }{4}} \right) = \sin \left( {\dfrac{\pi }{4}} \right) + \cos \left( {\dfrac{\pi }{4}} \right) = 1\]
Also, at \[x = \dfrac{{5\pi }}{4}\] , we have
\[ \Rightarrow f''\left( x \right) = 1 > 0\]
Hence it has local minima at \[x = \dfrac{{5\pi }}{4}\] .
That is,
\[ \Rightarrow f\left( {\dfrac{{5\pi }}{4}} \right) = \sin \left( {\dfrac{{5\pi }}{4}} \right) + \cos \left( {\dfrac{{5\pi }}{4}} \right) = - 1\]
Now, we have to check the nature of the function after \[0,\dfrac{\pi }{4},\dfrac{{5\pi }}{4}\] .
The sign chart for the function \[f\left( x \right) = \sin x + \cos x\] can be shown as:
| Interval | Sign of | Nature of \[f\left( x \right)\] |
| \[\left[ {0,\left. {\dfrac{\pi }{4}} \right)} \right.\] | negative | Increasing |
| \[\left( {\dfrac{\pi }{4},\dfrac{{5\pi }}{4}} \right)\] | positive | Decreasing |
| \[\left( {\dfrac{{5\pi }}{4}} \right.,\left. {2\pi } \right]\] | negative | Increasing |
Now for the concavity of \[f\left( x \right) = \sin x + \cos x\] , we have \[f''\left( x \right) = 0\] , that gives us
That gives,
\[ \Rightarrow \sin x = - \cos x\]
The values which satisfy above condition are,
\[ \Rightarrow x = \dfrac{{3\pi }}{4},\dfrac{{7\pi }}{4}\]
These are the inflection points.
Again, the sign chart for the concavity of the function \[f\left( x \right) = \sin x + \cos x\] can be shown as:
| Interval | Sign of | Concavity |
| \[\left[ 0 \right.,\left. {\dfrac{{3\pi }}{4}} \right)\] | Negative | Concave Down |
| \[\left( {\dfrac{{3\pi }}{4},\dfrac{{7\pi }}{4}} \right)\] | Positive | Concave Up |
| \[\left( {\dfrac{{7\pi }}{4},\left. {2\pi } \right]} \right.\] | Negative | Concave Down |
Note: We can also draw the graph of the function \[f\left( x \right) = \sin x + \cos x\] which shows the concavity and as well as the increasing decreasing nature of the given trigonometric function.

Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




