Question

Find if the following statement is true?
Tangent at any point P of the parabola bisects the angle between the focal chord through P and perpendicular from P to the directrix.

Answer 1

Hint: We start solving this problem by first assuming the parabola as ${{y}^{2}}=4ax$ and point P as $P\left( a{{t}^{2}},2at \right)$ and then drawing the rough figure of the given information. We assume the angle made by tangent with the perpendicular from point P to the directrix as $\alpha $ and the angle between tangent and focal chord as $\beta $. Then we take the slope of the tangent to the parabola at point P and then equate it to $\tan \alpha $ as they are alternate angles. Then we find the slope of focal chord PS using the formula, $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$. Then we use the formula $\tan \theta =\left| \dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}} \right|$ to find the angle between the tangent and the focal chord at P. Then we equate it to $\beta $. Then we check if the angles $\alpha $ and $\beta $ are equal and answer correspondingly.

Complete step by step answer:
Let us consider any parabola ${{y}^{2}}=4ax$.
Now let us consider some arbitrary point on the above parabola say $P\left( a{{t}^{2}},2at \right)$, $t>0$.
Now let us draw a chord from point P to the focus of the parabola, S$\left( a,0 \right)$ and perpendicular from point P to the directrix.
Let us assume that the angle made by tangent with the perpendicular from point P to the directrix as $\alpha $ and angle between the tangent and focal chord be $\beta $.
Then the rough figure looks like,

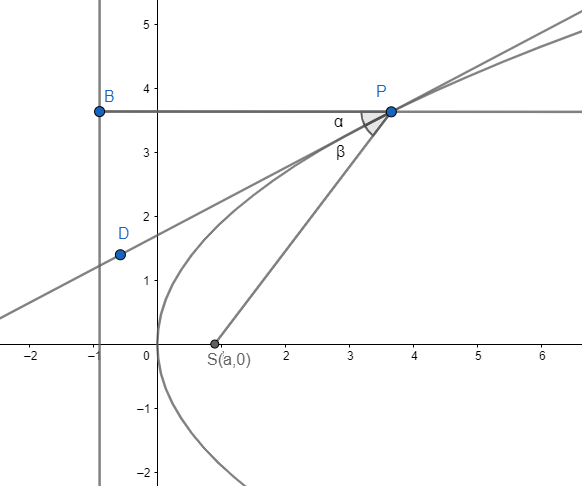
So, now let us find the value of $\alpha $ and $\beta $.
Let us consider the equation of tangent at point P, on this parabola,
$yt=x+a{{t}^{2}}.........\left( 1 \right)$
Now we can see in the figure that $\angle BPD=\alpha $. As it is the angle made by the tangent with the x-axis, we can say that tangent of it is equal to the slope of the tangent at P.
From equation (1), we can say that slope of the tangent is equal to $\dfrac{1}{t}$.
So, we get,
$\Rightarrow \tan \alpha =\dfrac{1}{t}.........\left( 2 \right)$
Now we need to find the angle between the tangent and the focal chord.
First let us find the slope of the focal chord PS.
Now let us consider the formula for slope of the line through points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$,
$m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
So, using it we get the slope of line PS as,
$\begin{align}
  & \Rightarrow m=\dfrac{2at-0}{a{{t}^{2}}-a} \\
 & \Rightarrow m=\dfrac{2at}{a\left( {{t}^{2}}-1 \right)} \\
 & \Rightarrow m=\dfrac{2t}{{{t}^{2}}-1} \\
\end{align}$
Now let us consider the formula for angle between two lines with slopes ${{m}_{1}}$ and ${{m}_{2}}$,
$\tan \theta =\left| \dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}} \right|$
So, applying this formula for angle between tangent and the focal chord with slopes, $\dfrac{1}{t}$ and $\dfrac{2t}{{{t}^{2}}-1}$, which is equal to $\beta $, we get,
$\Rightarrow \tan \beta =\left| \dfrac{\dfrac{1}{t}-\dfrac{2t}{{{t}^{2}}-1}}{1+\left( \dfrac{2t}{{{t}^{2}}-1} \right)\left( \dfrac{1}{t} \right)} \right|$
$\Rightarrow \tan \beta =\left| \dfrac{\dfrac{{{t}^{2}}-1-2{{t}^{2}}}{t\left( {{t}^{2}}-1 \right)}}{1+\dfrac{2}{{{t}^{2}}-1}} \right|$
$\begin{align}
  & \Rightarrow \tan \beta =\left| \dfrac{\dfrac{-1-{{t}^{2}}}{t\left( {{t}^{2}}-1 \right)}}{\dfrac{{{t}^{2}}+1}{{{t}^{2}}-1}} \right| \\
 & \Rightarrow \tan \beta =\left| \dfrac{-\left( 1+{{t}^{2}} \right)}{t\left( {{t}^{2}}+1 \right)} \right| \\
 & \Rightarrow \tan \beta =\left| \dfrac{-1}{t} \right| \\
\end{align}$
As $t>0$, we get,
$\Rightarrow \tan \beta =\dfrac{1}{t}...........\left( 3 \right)$
Now comparing the equations (2) and (3), we get that,
$\Rightarrow \tan \beta =\tan \alpha $
So, we get that
$\Rightarrow \alpha =\beta $
So, we can say that angle made by the tangent at point P with the focal chord from P and the perpendicular from P to the directrix are equal.
It means that the tangent at the point P of the parabola bisects the angle between the focal chord through P and perpendicular from P to the directrix.
So, the given statement is True.
Hence answer is True.

Note:
The common mistake take one makes while solving this problem is one might take the formula for the angle between two lines with slopes ${{m}_{1}}$ and ${{m}_{2}}$ as $\tan \theta =\dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}}$, that is without modulus. In that case they will get the answer as $\tan \beta =\dfrac{-1}{t}$ and mark the statement as false.