Question

How do you find horizontal asymptotes for \[f\left( x \right)={{\tan }^{-1}}\left( x \right)\] ?

Answer 1

Hint: To solve these types of problems efficiently, one has to have a fair knowledge of graph theory and asymptotes of a graph. Knowledge of inverse functions is also necessary. Asymptotes are defined as the lines, which meet a curve at infinity. In these types of questions, we first plot the graph for the original trigonometric function, here which is \[\tan \left( x \right)\] and then take its reflection about the line \[y=x\] to draw the graph of its inverse function. This is pretty much the straight forward rule to draw the graph for inverse functions.

Complete step by step answer:
Now starting off with the problem, we know that, when we try to calculate the value of \[\tan \left( \dfrac{\pi }{2} \right)\] or \[\tan \left( -\dfrac{\pi }{2} \right)\] or \[\tan \left( \dfrac{n\pi }{2} \right)\] (where ‘n’ is any integer, positive or negative), it comes out to be undefined, which means that the vertical line \[x=n\dfrac{\pi }{2}\] is an asymptote of the curve \[\tan \left( x \right)\] . Now since the reflection of the curve \[y=\tan \left( x \right)\] about the line \[y=x\] gives the graph for the inverse curve that is \[y={{\tan }^{-1}}\left( x \right)\], reflection of \[x=n\dfrac{\pi }{2}\] about the line \[y=x\] will also give the required equation of the horizontal asymptote. Thus we can safely say that \[y={{\tan }^{-1}}\left( \infty \right)\] and \[y={{\tan }^{-1}}\left( -\infty \right)\] will be the equations of the horizontal asymptotes of the equation \[y={{\tan }^{-1}}\left( x \right)\] . We can further write that \[y={{\tan }^{-1}}\left( \tan \left( \dfrac{n\pi }{2} \right) \right)\] is the general equation for the asymptote. Thus,
\[y=\dfrac{n\pi }{2}\] , is the equation of the horizontal asymptote, where ‘n’ is any integer, positive or negative.

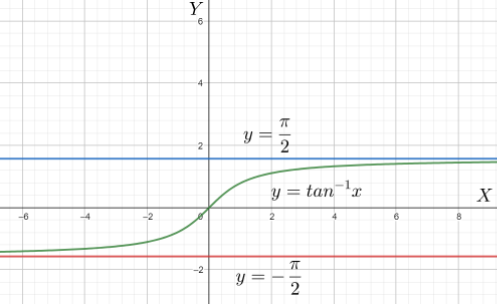
Note: We have to be very careful regarding the domain and range of the problem. In this question since no domain and range is given, the method done here is a more generalized one. After plotting the graph, we need to closely analyse for the lines which may meet the graph at infinity.