Question

Find five rational numbers between -1 and 1.

Answer 1

Hint: We must first understand what are meant by rational numbers. Any number that can be expressed in the form $\dfrac{p}{q}$, where p and q are integers and q is not equal to 0 is called a rational number. Using this definition, we can analyse different numbers and select which ones are rational.

Complete step-by-step solution:
We know that any number of the form $\dfrac{p}{q}$, where p and q are integers and q is not equal to 0 is called a rational number.
So, we can say that all those numbers that can not be expressed in the form $\dfrac{p}{q}$, where p and q are integers and q is not equal to 0, are called irrational numbers.
In this question, we need to find five rational numbers between -1 and 1.
Let us represent these two numbers on the number line.

Let us have a look at the number 0.
We know that we can represent 0 in the form $\dfrac{0}{1}$. Here, 0 and 1, both are integers and 1 is not equal to 0. Thus, 0 is a rational number lying between -1 and 1.
We can also see that in $\dfrac{1}{2}$, 1 and 2 both are integers and 2 is not equal to 0. So, $\dfrac{1}{2}$ is also a rational number between -1 and 1.
For the number $\dfrac{-1}{2}$, we can see that -1 and 2 both are integers and 2 is not equal to 0. So, $-\dfrac{1}{2}$ is also a rational number between -1 and 1.
We can also see that in $\dfrac{1}{4}$, 1 and 4 both are integers and 4 is not equal to 0. So, $\dfrac{1}{4}$ is also a rational number between -1 and 1.
In the number $\dfrac{-1}{4}$, -1 and 4 both are integers and 4 is not equal to 0. So, $-\dfrac{1}{4}$ is also a rational number between -1 and 1.

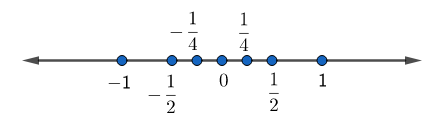
Hence, the numbers $-\dfrac{1}{2},\text{ }-\dfrac{1}{4},\text{ }0,\text{ }\dfrac{1}{4}\text{ and }\dfrac{1}{2}$ are five rational numbers between -1 and 1.

Note: We must remember that there can be an infinite number of rational numbers between any two given numbers. Hence, there can be an infinite number of possible solutions for this problem. Also, since nothing is specifically said, we must not consider the numbers -1 and 1 in our solution.