
Find distance of centre of mass of ${{H}_{2}}0$ molecule.
Answer
564.9k+ views
Hint: In order to solve this question, you must first know the structure of the structure${{H}_{2}}0$ molecule. The ${{H}_{2}}0$ molecule is formed by the two hydrogen atoms and an oxygen atom. The distance between the hydrogen atom and oxygen atom is $0.96\times {{10}^{-10}}m$. Forming an angle of \[{{104}^{\circ }}\].
The mass of one hydrogen atom is 1 unit and the mass of an oxygen atom is 16 units. Using these data, one can easily calculate the centre of mass by simply applying the same in the formula for the centre of mass.
Complete answer:
Before we start solving the question, let us take a look at the molecular structure of ${{H}_{2}}0$ molecule.
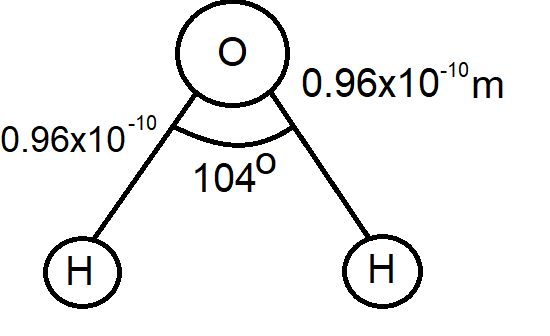
Now,
We can see that it is in form of a triangle
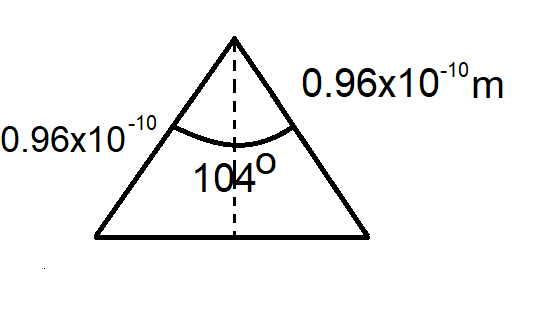
Now, as we know that
Mass of a hydrogen atom = 1 unit
And, the mass of one oxygen atom will be 16 unit
So, now
Let the distance between the hydrogen atom and oxygen atom be d
Then
$d=0.96\times {{10}^{-10}}m$
So,
By the formula,
\[{{X}_{CM}}=\dfrac{{{m}_{1}}+{{m}_{2}}{{x}_{2}}+{{m}_{3}}{{x}_{3}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\]
Now,
Using the values we have in the above formula, we have
\[\Rightarrow {{X}_{CM}}=\dfrac{-d\sin {{52}^{\circ }}+d\sin {{52}^{\circ }}+16\times 0}{1+1+16}\]
\[\Rightarrow {{X}_{CM}}=0\]
Now,
\[\Rightarrow {{Y}_{CM}}=\dfrac{{{m}_{1}}+{{m}_{2}}{{y}_{2}}+{{m}_{3}}{{y}_{3}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\]
\[\Rightarrow {{Y}_{CM}}=\dfrac{0+0+16\times 0.96\times {{10}^{-10}}\cos {{52}^{\circ }}}{1+1+16}\]
\[\Rightarrow {{Y}_{CM}}=\dfrac{8}{9}\times 0.96\times {{10}^{-10}}\cos {{52}^{\circ }}\]
So, we will have the coordinates of the centre of mass as (0, \[\dfrac{8}{9}\times 0.96\times {{10}^{-10}}\cos {{52}^{\circ }}\])
Note:
In this question we have the answer in form of coordinates, it means the centre of mass is at a distance of \[\dfrac{8}{9}\times 0.96\times {{10}^{-10}}\cos {{52}^{\circ }}\]m away from the centre of the line joining the two hydrogen atom.
One interesting fact about The ${{H}_{2}}0$ molecule is that is forms hydrogen bond, which is a special type of bond only formed when a hydrogen atom is covalently bonded to a very electronegative atom such as a N, O, or F atom and another very electronegative atom.
The mass of one hydrogen atom is 1 unit and the mass of an oxygen atom is 16 units. Using these data, one can easily calculate the centre of mass by simply applying the same in the formula for the centre of mass.
Complete answer:
Before we start solving the question, let us take a look at the molecular structure of ${{H}_{2}}0$ molecule.

Now,
We can see that it is in form of a triangle
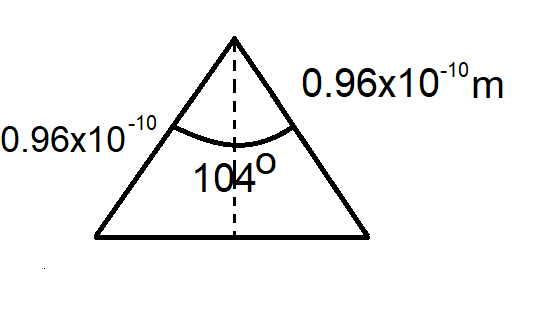
Now, as we know that
Mass of a hydrogen atom = 1 unit
And, the mass of one oxygen atom will be 16 unit
So, now
Let the distance between the hydrogen atom and oxygen atom be d
Then
$d=0.96\times {{10}^{-10}}m$
So,
By the formula,
\[{{X}_{CM}}=\dfrac{{{m}_{1}}+{{m}_{2}}{{x}_{2}}+{{m}_{3}}{{x}_{3}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\]
Now,
Using the values we have in the above formula, we have
\[\Rightarrow {{X}_{CM}}=\dfrac{-d\sin {{52}^{\circ }}+d\sin {{52}^{\circ }}+16\times 0}{1+1+16}\]
\[\Rightarrow {{X}_{CM}}=0\]
Now,
\[\Rightarrow {{Y}_{CM}}=\dfrac{{{m}_{1}}+{{m}_{2}}{{y}_{2}}+{{m}_{3}}{{y}_{3}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\]
\[\Rightarrow {{Y}_{CM}}=\dfrac{0+0+16\times 0.96\times {{10}^{-10}}\cos {{52}^{\circ }}}{1+1+16}\]
\[\Rightarrow {{Y}_{CM}}=\dfrac{8}{9}\times 0.96\times {{10}^{-10}}\cos {{52}^{\circ }}\]
So, we will have the coordinates of the centre of mass as (0, \[\dfrac{8}{9}\times 0.96\times {{10}^{-10}}\cos {{52}^{\circ }}\])
Note:
In this question we have the answer in form of coordinates, it means the centre of mass is at a distance of \[\dfrac{8}{9}\times 0.96\times {{10}^{-10}}\cos {{52}^{\circ }}\]m away from the centre of the line joining the two hydrogen atom.
One interesting fact about The ${{H}_{2}}0$ molecule is that is forms hydrogen bond, which is a special type of bond only formed when a hydrogen atom is covalently bonded to a very electronegative atom such as a N, O, or F atom and another very electronegative atom.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Explain zero factorial class 11 maths CBSE

What is a periderm How does periderm formation take class 11 biology CBSE




