Question

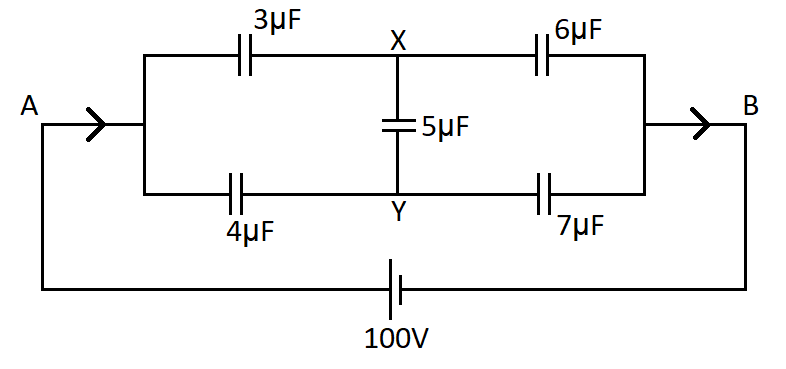
Find ${C_{AB}}$.

Answer 1

Hint
To find a solution to this problem, we need to find the potentials at point X and Y in the figure. Then using those potentials we need to find the charge that is flowing from the point B to A. So then using the charge and the potential between points A and B we can find the capacitance ${C_{AB}}$.
In this solution we will be using the following formula,
$\Rightarrow Q = CV$
where $Q$ is the charge, $V$ is the potential and $C$ is the capacitance of a capacitor.

Complete step by step answer
Here we need to use the nodal analysis and by distribution of potential to find the equivalent capacitance across the unbalanced Wheatstone bridge.

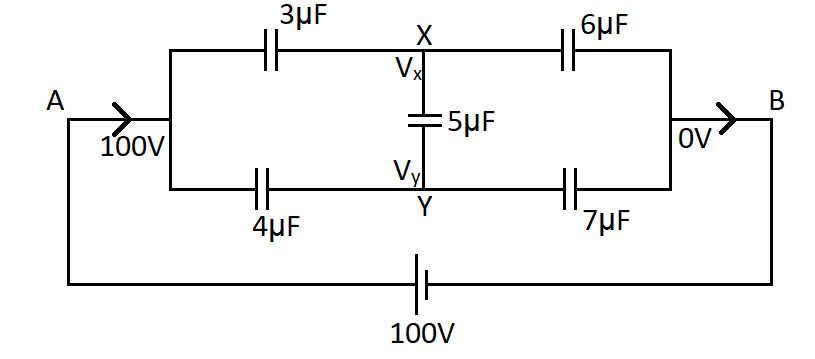
According to the problem, the potential at the point A in the circuit is $100V$ and at the point B the potential is $0V$. And let the potential at the nodes X and Y is ${V_X}$ and ${V_Y}$ respectively.
Now at the node X we know that the sum of the charges on all the plates should be equal to zero. And similarly at the node Y the sum of the charges is zero.
Now we know that the charge on the plate of capacitor is given by
$\Rightarrow Q = CV$
At the node X, the charges will be due to the right plate of $3\mu F$ capacitor, left plate of the $6\mu F$ and the top plate of the $5\mu F$. The charges of these plates are given by the product of their capacitance and potential.
So for the $3\mu F$ capacitor, charge on right plate is $3\left( {{V_X} - 100} \right)$ and for the $6\mu F$ capacitor, charge on the left plate is $6\left( {{V_X} - 0} \right)$. For the $5\mu F$ capacitor, charge on top plate is, $5\left( {{V_X} - {V_Y}} \right)$
Now the sum of these charges is zero. Therefore we can write,
$\Rightarrow 3\left( {{V_X} - 100} \right) + 6\left( {{V_X} - 0} \right) + 5\left( {{V_X} - {V_Y}} \right) = 0$
We can simplify this equation as,
$\Rightarrow 3{V_X} + 6{V_X} + 5{V_X} - 5{V_Y} = 300$
On adding the values we get
$\Rightarrow 14{V_X} - 5{V_Y} = 300$. This is the equation 1.
Similarly at the node Y, the charges will be due to the right plate of $4\mu F$ capacitor, left plate of the $7\mu F$ and the bottom plate of the $5\mu F$. The charges of these plates are given by the product of their capacitance and potential.
So for the $4\mu F$ capacitor, charge on right plate is $4\left( {{V_Y} - 100} \right)$ and for the $7\mu F$ capacitor, charge on the left plate is $7\left( {{V_Y} - 0} \right)$. For the $5\mu F$ capacitor, charge on bottom plate is, $5\left( {{V_Y} - {V_X}} \right)$
Now the sum of these charges is zero. Therefore we can write,
$\Rightarrow 4\left( {{V_Y} - 100} \right) + 7\left( {{V_Y} - 0} \right) + 5\left( {{V_Y} - {V_X}} \right) = 0$
We can simplify this equation as,
$\Rightarrow 4{V_Y} + 7{V_Y} + 5{V_Y} - 5{V_X} = 400$
On adding the common terms we get
$\Rightarrow - 5{V_X} + 16{V_Y} = 400$. This is equation 2.
Now equation 1 and 2 are simultaneous equations. So to solve them,
$\Rightarrow \left( {14{V_X} - 5{V_Y} = 300} \right) \times 5$
$\Rightarrow \left( { - 5{V_X} + 16{V_Y} = 400} \right) \times 14$
So we get the equations as,
$\Rightarrow 70{V_X} - 25{V_Y} = 1500$
$\Rightarrow - 70{V_X} + 224{V_Y} = 5600$
Now we perform addition on the above 2 equations, hence we get,
$\Rightarrow 70{V_X} - 25{V_Y} - 70{V_X} + 224{V_Y} = 1500 + 5600$
So on cancelling the terms containing ${V_X}$ and adding rest of the common terms,
$\Rightarrow 199{V_Y} = 7100$
Therefore, from here we get the value of ${V_Y}$ as,
$\Rightarrow {V_Y} = \dfrac{{7100}}{{199}} = 35.67V$
And we get the value of ${V_X}$ by substituting ${V_Y}$ in $ - 5{V_X} + 16{V_Y} = 400$ as,
$\Rightarrow - 5{V_X} + 16 \times 35.67 = 400$
This gives us,
$\Rightarrow 5{V_X} = 570.72 - 400$
Therefore we get the value of ${V_X}$ as
$\Rightarrow {V_X} = 34.14V$
The positive charges in the circuit move from the point B in the circuit to the point A along the arrow. So we can say that the small amount of charges given by $\Delta Q$ moves from the right plate of the $6\mu F$ and $7\mu F$ capacitors to the left plate of $3\mu F$ and $4\mu F$ capacitors.
So this charge can be calculated as the sum of charges leaving $6\mu F$ and $7\mu F$ capacitors.
Therefore, $\Delta Q = 6\left( {{V_X} - 0} \right) + 7\left( {{V_Y} - 0} \right)$
So we get, $\Delta Q = 6{V_X} + 7{V_Y}$
Substituting the previously obtained values of ${V_X}$ and ${V_Y}$ we get,
$\Rightarrow \Delta Q = \left( {6 \times 34.14} \right) + \left( {7 \times 35.67} \right)$
On doing the above calculation we obtain the charge as, $\Delta Q = 454.53\mu C$
Hence in this whole circuit, the charge moving from B to A is $\Delta Q = 454.53\mu C$ and the potential across B and A is $V = 100V$. So using these two values we can find the value of the capacitance between A and B as,
$\Rightarrow {C_{AB}} = \dfrac{{\Delta Q}}{V}$
Substituting the values we get,
$\Rightarrow {C_{AB}} = \dfrac{{454.53}}{{100}} = 4.54\mu F$.

Note
If the capacitances across the Wheatstone bridge were in balanced condition, that is ,
$\dfrac{{{C_1}}}{{{C_2}}} = \dfrac{{{C_3}}}{{{C_4}}}$, then the potential across the capacitor in the middle would have become insignificant as the potential difference across that capacitor would have become zero. And we could have calculated the equivalent capacitance.