Question

Find by integration, the area bounded by the curve $y=2x-{{x}^{2}}$ and the x-axis.

Answer 1

Hint: Plot the curve on a graph. Use the fact that the area bounded by the curve y = f(x), the x-axis, and the ordinates x= a and x = b is given by $\int_{a}^{b}{\left| f\left( x \right) \right|dx}$. Argue that the required area is the area bounded by the curve $y=2x-{{x}^{2}}$, the x-axis and the ordinates x= 0 and x= 2.Hence prove that the required area is $\int_{0}^{2}{\left( 2x-{{x}^{2}} \right)dx}$. Integrate and hence find the required area.

Complete step-by-step answer:

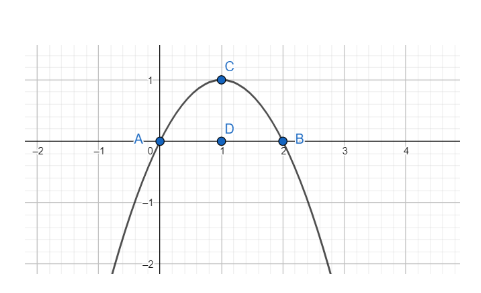
As is evident from the graph, the area bound the curve $y=2x-{{x}^{2}}$ is equal to the area ACBDA.
Finding the coordinates of A and B:
As is evident from the A and B are the roots of $f\left( x \right)=2x-{{x}^{2}}$
Hence, we have
$2x-{{x}^{2}}=0\Rightarrow x=0,2$
Hence, we have $A\equiv \left( 0,0 \right)$ and $B\equiv \left( 2,0 \right)$
Hence the area ACBDA is the area bounded by the curve $y=2x-{{x}^{2}}$, the x-axis and the ordinates x= 0 and x= 2.
We know that the area bounded by the curve y = f(x), the x-axis, and the ordinates x= a and x = b is given by $\int_{a}^{b}{\left| f\left( x \right) \right|dx}$
Hence, we have
Required area $=\int_{0}^{2}{\left| 2x-{{x}^{2}} \right|}dx$
Now, we have $2x-{{x}^{2}}=x\left( 2-x \right)$
In the interval (0,2), we have x and 2-x both are non-negative
Hence, we have $x\left( 2-x \right)\ge 0$
Hence, we have
$\left| x\left( 2-x \right) \right|=x\left( 2-x \right)$
Hence, we have
Required area $=\int_{0}^{2}{\left( 2x-{{x}^{2}} \right)dx}=\left. {{x}^{2}}-\dfrac{{{x}^{3}}}{3} \right|_{0}^{2}=\left( 4-\dfrac{8}{3} \right)=\dfrac{4}{3}$ square units.

Note: Alternative use the fact that the area bounded by the curve $y=C\left( x-a \right)\left( x-b \right)$ and the x-axis is given by $\dfrac{\left| C \right|{{\left( a-b \right)}^{3}}}{6}$
Here, we have $2x-{{x}^{2}}=-\left( x-0 \right)\left( x-2 \right)$
Hence a = 0, b = 2 and C =-1
Hence the required area is $\dfrac{\left| -1 \right|{{\left( 2-0 \right)}^{3}}}{6}=\dfrac{8}{6}=\dfrac{4}{3}$, which is the same as obtained above.