Question

How to find bond angle of ${\text{N}}{{\text{H}}_{\text{3}}}$, ${\left( {{\text{B}}{{\text{F}}_{\text{4}}}} \right)^ - }$?

Answer 1

Hint:To find the bond angle first determine the geometry of the given molecules i.e. ${\text{N}}{{\text{H}}_{\text{3}}}$ and ${\left( {{\text{B}}{{\text{F}}_{\text{4}}}} \right)^ - }$. The geometry of the molecules can be determined by drawing the Lewis structures of these molecules. To draw the Lewis structure first calculate the valence electrons for the molecules.

Complete answer:
We will calculate the valence electrons of ${\text{N}}{{\text{H}}_{\text{3}}}$ molecule as follows:-
The valence electrons of nitrogen are 5 and the valence electrons of hydrogen are 1. Thus,
Valence electrons of ${\text{N}}{{\text{H}}_{\text{3}}}$ $ = \left( {1 \times {\text{Valence electrons of N}}} \right) + \left( {3 \times {\text{Valence electrons of H}}} \right)$
$ = \left( {1 \times 5} \right) + \left( {3 \times 1} \right)$
$ = 5 + 3$
Valence electrons of ${\text{N}}{{\text{H}}_{\text{3}}}$ $ = 8$
Draw the Lewis structure of ${\text{N}}{{\text{H}}_{\text{3}}}$ as follows:
The structure of ${\text{N}}{{\text{H}}_{\text{3}}}$ is,

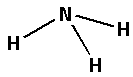
The three hydrogen atoms bond with one nitrogen atom forming three bonds. As three bonds are formed, six electrons are involved in bonding. Thus, the remaining electrons are,
Remaining electrons $ = 8 - 6 = 2$
Place the remaining 2 electrons around the nitrogen atom so that the nitrogen atom completes its octets. Thus,

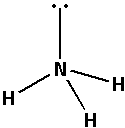
The structure of ${\text{N}}{{\text{H}}_{\text{3}}}$ has three electron bond pairs and one electron lone pair on the central nitrogen atom. Thus, the geometry of ${\text{N}}{{\text{H}}_{\text{3}}}$ molecule is trigonal pyramidal.
As there is one electron lone pair there occurs more repulsion between the electron bond pair and electron lone pair. This causes a reduction in the bond angle. The bond angle reduces from ${109.5^ \circ }$ to \[{107^ \circ }\]. Thus, the bond angle of ${\text{N}}{{\text{H}}_{\text{3}}}$ is \[{107^ \circ }\].
Calculate the valence electrons of ${\left( {{\text{B}}{{\text{F}}_{\text{4}}}} \right)^ - }$ molecule as follows:
The valence electrons of boron are 3 and the valence electrons of fluorine are 7. Thus,
Valence electrons of ${\left( {{\text{B}}{{\text{F}}_{\text{4}}}} \right)^ - }$ $ = \left( {1 \times {\text{Valence electrons of B}}} \right) + \left( {4 \times {\text{Valence electrons of F}}} \right) + 1$
$ = \left( {1 \times 3} \right) + \left( {4 \times 7} \right) + 1$
$ = 3 + 28 + 1$
Valence electrons of ${\left( {{\text{B}}{{\text{F}}_{\text{4}}}} \right)^ - }$ $ = 32$
Draw the Lewis structure of ${\left( {{\text{B}}{{\text{F}}_{\text{4}}}} \right)^ - }$ as follows:
The structure of ${\left( {{\text{B}}{{\text{F}}_{\text{4}}}} \right)^ - }$ is,

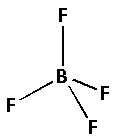
The four fluorine atoms bond with one boron atom forming four bonds. As four bonds are formed, eight electrons are involved in bonding. Thus, the remaining electrons are,
Remaining electrons $ = 32 - 8 = 24$
Place the remaining 24 electrons around the fluorine atoms so that the fluorine atoms complete their octets. Thus,

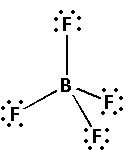
The structure of ${\left( {{\text{B}}{{\text{F}}_{\text{4}}}} \right)^ - }$ has four electron bond pairs on the central boron atom. Thus, the geometry of ${\left( {{\text{B}}{{\text{F}}_{\text{4}}}} \right)^ - }$ molecule is tetrahedral. Thus, the bond angle of ${\left( {{\text{B}}{{\text{F}}_{\text{4}}}} \right)^ - }$ is \[{109.5^ \circ }\].

Note:Remember that the structure of ${\text{N}}{{\text{H}}_{\text{3}}}$ has three electron bond pairs and one electron lone pair on the central nitrogen atom. Thus, the geometry of ${\text{N}}{{\text{H}}_{\text{3}}}$ molecule is trigonal pyramidal. As there is one electron lone pair there occurs more repulsion between the electron bond pair and electron lone pair. This causes a reduction in the bond angle. The bond angle reduces from ${109.5^ \circ }$ to \[{107^ \circ }\]. Thus, the bond angle of ${\text{N}}{{\text{H}}_{\text{3}}}$ is \[{107^ \circ }\].