Question

How to find area of a circle inside a square with side $4$?

Answer 1

Hint: Here the circle is inscribed the square, first of all we will draw the diagram and then observe it that gives us that the radius of the circle is half of the side and then apply the area of the circle for the resultant value.

Complete step-by-step answer:
First of all draw the figure with the circle inscribed in the square,

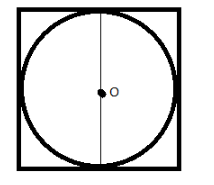
Now, here we can observe that the radius of the circle is half of the measure of the side of the square.
Therefore, radius $r = \dfrac{4}{2} = 2$unit
Now, the area of the circle can be given as –
$A = \pi {r^2}$
Place the known values, also $\pi = 3.14$
$A = (3.14){(2)^2}$
Simplify the above expression finding the product of the terms on the right hand side of the above equation –
$A = 12.56$ square units
This is the required solution.
So, the correct answer is “$A = 12.56$ square units”.

Note: Know the difference between the circumscribed and inscribed. The circumcircle of the square is the point where the two diagonals of the square meet and is made through the four vertices of the square whereas, incircle of the square is when the circle is inscribed in the square. Also, remember the standard formulas for the areas of the closed figure. Do not forget to write the appropriate units to the resultant value.