Question

Find angle “x” if:

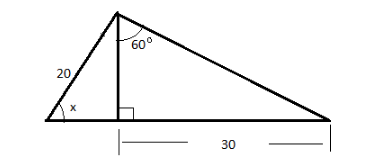
Answer 1

Hint: Here we will use different trigonometric functions relating the sides of the triangle. Here we will use tangent as the opposite side to the adjacent side and the cosine as the ratio of opposite sides with the hypotenuse. Place the values and find the correlation between the two for the required value.

Complete step-by-step answer:
First of all entitle the given diagram.

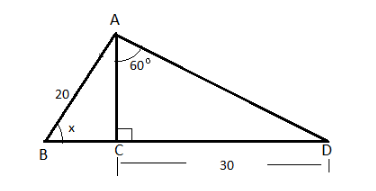
Let us assume that the distance AC be “h”
We know that the trigonometric function tangent is the ratio of opposite side to adjacent side.
 $ \tan 60^\circ = \dfrac{{CD}}{{AC}} $
Place values in the above equation – $ \tan 60^\circ = \sqrt 3 $ and $ CD = 30 $
 $ \sqrt 3 = \dfrac{{30}}{h} $
Do cross multiplication –
 $ \Rightarrow h = \dfrac{{30}}{{\sqrt 3 }} $
Now, from the figure we can use cosine function as it is on the opposite side of the hypotenuse.
 $ \cos x = \dfrac{{AC}}{{AB}} $
Place values in the above equation –
 $ \cos x = \dfrac{h}{{20}} $
Place, $ h = \dfrac{{30}}{{\sqrt 3 }} $ in the above equation –
 $ \cos x = \dfrac{{\dfrac{{30}}{{\sqrt 3 }}}}{{20}} $
Remember the numerator’s denominator goes to the denominator. Simplify the above equation.
 $ \Rightarrow \cos x = \dfrac{{30}}{{\sqrt 3 \times 20}} $
Find the factors from the numerator and the denominator –
 $ \Rightarrow \cos x = \dfrac{{3 \times 10}}{{\sqrt 3 \times 2 \times 10}} $
Common factors from the numerator and the denominator cancel each other. Therefore remove from the numerator and the denominator.
 $ \Rightarrow \cos x = \dfrac{3}{{\sqrt 3 \times 2}} $
Again, by using the property of square and square-root –
 $ \Rightarrow \cos x = \dfrac{{\sqrt 3 \times \sqrt 3 }}{{\sqrt 3 \times 2}} $
Common factors from the numerator and the denominator cancel each other. Therefore remove from the numerator and the denominator.
 $ \Rightarrow \cos x = \dfrac{{\sqrt 3 }}{2} $
Write the trigonometric function for the value. As we know that $ \cos 30^\circ = \dfrac{{\sqrt 3 }}{2} $
 $ \cos x = \cos 30^\circ $
By comparing both the sides of the equation –
 $ \Rightarrow x = 30^\circ $
So, the correct answer is “ $ x = 30^\circ $ ”.

Note: Always remember the trigonometric table for the values of the different angles for sine and cosine for the efficient and the accurate solution. Also, be careful while simplifying the equations. Also, be wise while applying the identities of square and square-root.