Question

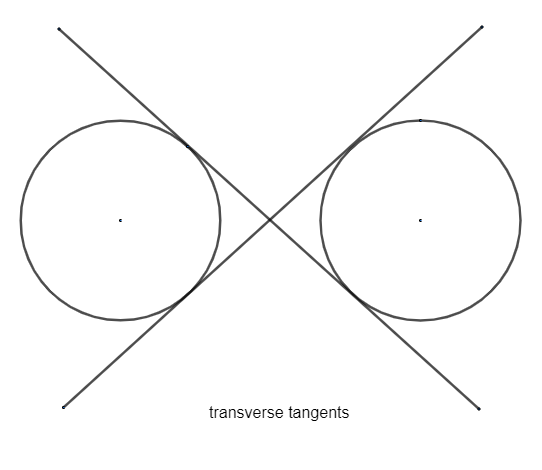
Find and draw a transverse common tangent to two circles of radii 6cm and 2cm whose centres are 8cm apart.

Answer 1

Hint: Derive the length of a transverse tangent in terms of radii of both the circle and the distance between their centres. Radii joining the transverse tangent will be parallel to each other. And use the concept that if the sum of radii of both the circles is equal to distance between centres then they will touch each other.
Complete step-by-step answer:
Let us derive the relation to get the length common transverse tangent for two circles. So, length of transverse tangent can be calculated as

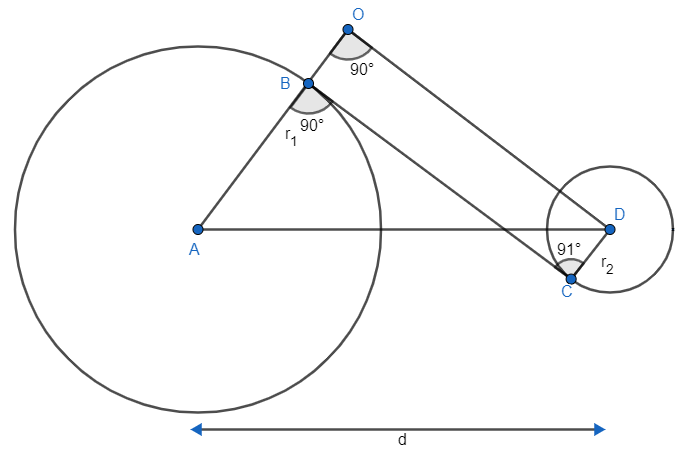
Now, as we know radius and tangent are perpendicular to each other at the point of tangency and we also know there is only one perpendicular direction for any line i.e. direction of perpendicular to any line will be unique.
As, $AB\bot BC,CD\bot BC\Rightarrow AB||CD$ because two perpendicular on the same line with two different directions is not possible. Now, proceed the radius AB (which is parallel to CD) to the length of CD i.e.
${{r}_{2}}\Rightarrow OB=CD,OB||CD$
From the diagram and two of the angles of quadrilateral
$\angle OBC=\angle DCB={{90}^{\circ }}$
Hence, ODCB will be a rectangle with equal opposite sides and all the angles of it will be ${{90}^{\circ }}$ so, $\angle ={{90}^{\circ }}$
Now, we know
$\begin{align}
  & OA=OB+AB \\
 & OA={{r}_{2}}+{{r}_{1}}..........................\left( i \right) \\
\end{align}$
In triangle OAD we can apply Pythagoras theorem as
${{\left( \text{Hypotenuse} \right)}^{2}}={{\left( \text{Base} \right)}^{2}}+{{\left( \text{Perpendicular} \right)}^{2}}$
$\begin{align}
  & A{{D}^{2}}=O{{A}^{2}}+O{{D}^{2}} \\
 & {{d}^{2}}={{\left( {{r}_{1}}+{{r}_{2}} \right)}^{2}}+O{{D}^{2}} \\
 & O{{D}^{2}}={{d}^{2}}-{{\left( {{r}_{1}}+{{r}_{2}} \right)}^{2}} \\
\end{align}$
As, OBCD is a rectangle, so, OD = BC. Hence, we can write above equation as
$B{{C}^{2}}={{d}^{2}}-{{\left( {{r}_{1}}+{{r}_{2}} \right)}^{2}}$
Transverse common tangent length as
$BC=\sqrt{{{d}^{2}}-{{\left( {{r}_{1}}+{{r}_{2}} \right)}^{2}}}..........................\left( ii \right)$
Now, coming to the question we are given two circles of radii 6cm and 2cm and distance between their centres is 8cm. So, we can apply the above mentioned result to get the length of the transverse common tangent. So, we get
$\text{Length of transverse tangent}=\sqrt{{{\left( d \right)}^{2}}-{{\left( {{r}_{1}}+{{r}_{2}} \right)}^{2}}}$
Where d is distance between centres and ${{r}_{1}},{{r}_{2}}$ are radii of the circle we know
$\begin{align}
  & {{r}_{1}}=6cm \\
 & {{r}_{2}}=2cm \\
 & d=2cm \\
\end{align}$
Hence, we get length of transverse common tangent as
$\begin{align}
  & \sqrt{{{\left( 8 \right)}^{2}}-{{\left( 2+6 \right)}^{2}}} \\
 & =0 \\
\end{align}$
Hence, no transverse tangent will touch each circle at one point where circles will touch each other as well. It can be observed by the relation among radii and distance between centres. We get,
$\begin{align}
  & {{r}_{1}}+{{r}_{2}}=d \\
 & 6+2=8 \\
 & 8=8 \\
\end{align}$
So, distance between centres is equal to the sum of their radii. It means both the circles will touch each other.

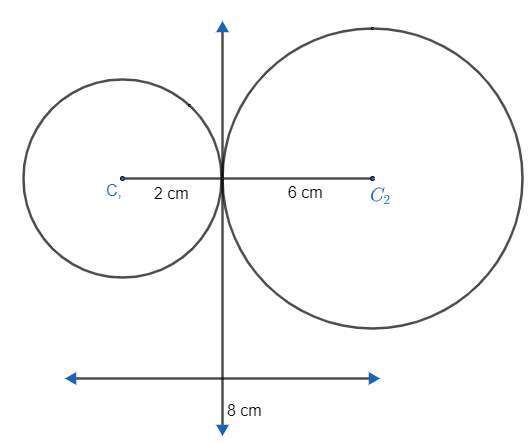
Note: We don’t need to derive a formula for length of transverse common tangent for the given circles as they are touching each other, so we can directly give the length as 0, but for the future reference and other problems of the same type, where circles will not meet. So, be clear with the formula as well.
Be clear with the transverse and direct common tangents. Both can be drawn as