Question

How do you find all zeros with multiplicities of $f\left( x \right)={{x}^{4}}-9{{x}^{2}}-4x+12$?

Answer 1

Hint: For this problem we need to calculate the zeros with multiplicities of the given equation. We can observe that the given equation is a quartic equation. For this equation we will calculate the value of the given function for $x=1,2,3,...$. Now we will check where the given function has the zero value for which value $x$ and it can be taken as the root of the given equation. Now we will reduce the given equation by dividing it with the obtained root. Now we will get a cubic equation, for this equation we will use rational root theorem and simplify the equation to get the required result.

Complete step by step solution:
Given that, $f\left( x \right)={{x}^{4}}-9{{x}^{2}}-4x+12$
Calculating the value of $f\left( 1 \right)$ by substituting $x=1$, in the above equation, then we will get
$\begin{align}
  & \Rightarrow f\left( 1 \right)={{\left( 1 \right)}^{4}}-9{{\left( 1 \right)}^{2}}-4\left( 1 \right)+12 \\
 & \Rightarrow f\left( 1 \right)=1-9-4+12 \\
 & \Rightarrow f\left( 1 \right)=0 \\
\end{align}$
Here we get the value of $f\left( 1 \right)$ as zero. So, we can write that $x-1$ is a factor of the given function and $1$ is the root of the function.
Dividing the given function with $x-1$, then we will get
$\begin{align}
  & 1\underline{\left| \begin{matrix}
   \begin{matrix}
   \begin{matrix}
   1 \\
   0 \\
\end{matrix} & \begin{matrix}
   0 \\
   1 \\
\end{matrix} \\
\end{matrix} & \begin{matrix}
   -9 \\
   1 \\
\end{matrix} & \begin{matrix}
   -4 \\
   -8 \\
\end{matrix} & \begin{matrix}
   12 \\
   -12 \\
\end{matrix} \\
\end{matrix} \right.} \\
 & \begin{matrix}
   \text{ }\begin{matrix}
   1 & 1 \\
\end{matrix} & \text{ } \text{ } -8 & \text{ } -12 & \text{ } \text{ } \text{ } \text{ }0 \\
\end{matrix} \\
\end{align}$
$\Rightarrow f\left( x \right)=\left( x-1 \right)\left( {{x}^{3}}+{{x}^{2}}-8x-12 \right)$
Now considering the cubic equation ${{x}^{3}}+{{x}^{2}}-8x-12$.
From the rational root’s theorem, we can write the possible roots of the above cubic equation as
$\pm 1$, $\pm 2$, $\pm 3$, $\pm 4$, $\pm 6$, $\pm 12$.
Checking whether the $1$ is root or not by substituting it in the cubic equation, then we will get
$\begin{align}
  & \Rightarrow {{x}^{3}}+{{x}^{2}}-8x-12={{1}^{3}}+{{1}^{2}}-8\left( 1 \right)-12 \\
 & \Rightarrow {{x}^{3}}+{{x}^{2}}-8x-12=1+1-8-12 \\
 & \Rightarrow {{x}^{3}}+{{x}^{2}}-8x-12=-18\ne 0 \\
\end{align}$
So $1$ is not a root of the cubic equation.
Checking whether the $-1$ is root or not by substituting it in the cubic equation, then we will get
$\begin{align}
  & \Rightarrow {{x}^{3}}+{{x}^{2}}-8x-12={{\left( -1 \right)}^{3}}+{{\left( -1 \right)}^{2}}-8\left( -1 \right)-12 \\
 & \Rightarrow {{x}^{3}}+{{x}^{2}}-8x-12=-1+1+8-12 \\
 & \Rightarrow {{x}^{3}}+{{x}^{2}}-8x-12=-4\ne 0 \\
\end{align}$
So $-1$ is not a root of the cubic equation.
Checking whether the $2$ is root or not by substituting it in the cubic equation, then we will get
$\begin{align}
  & \Rightarrow {{x}^{3}}+{{x}^{2}}-8x-12={{\left( 2 \right)}^{3}}+{{\left( 2 \right)}^{2}}-8\left( 2 \right)-12 \\
 & \Rightarrow {{x}^{3}}+{{x}^{2}}-8x-12=8+4-16-12 \\
 & \Rightarrow {{x}^{3}}+{{x}^{2}}-8x-12=-16\ne 0 \\
\end{align}$
So $2$ is not a root of the cubic equation.
Checking whether the $-2$ is root or not by substituting it in the cubic equation, then we will get
$\begin{align}
  & \Rightarrow {{x}^{3}}+{{x}^{2}}-8x-12={{\left( -2 \right)}^{3}}+{{\left( -2 \right)}^{2}}-8\left( -2 \right)-12 \\
 & \Rightarrow {{x}^{3}}+{{x}^{2}}-8x-12=-8+4+16-12 \\
 & \Rightarrow {{x}^{3}}+{{x}^{2}}-8x-12=0 \\
\end{align}$
Hence $-2$ is the root of the cubic equation.
Now we are going to divide the cubic equation with $x=-2$, then we will get
$\begin{align}
  & -2\underline{\left| \begin{matrix}
   \begin{matrix}
   1 \\
   0 \\
\end{matrix} & \begin{matrix}
   \text{ } \text{ } \text{ }1 \\
   -2 \\
\end{matrix} & \begin{matrix}
   -8 \\
   \text{ }2 \\
\end{matrix} & \begin{matrix}
   -12 \\
   \text{ } 12 \\
\end{matrix} \\
\end{matrix} \right.} \\
 & \text{ }\begin{matrix}
   \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{}1 & \text{}-1 & -6 & \text{ } \text{ } \text{ } \text{ }0 \\
\end{matrix} \\
\end{align}$Now we can write the given function as
$\Rightarrow f\left( x \right)=\left( x-1 \right)\left( x+2 \right)\left( {{x}^{2}}-x-6 \right)$
Considering the quadratic equation ${{x}^{2}}-x-6=0$.
We know that the roots of the quadratic equation $a{{x}^{2}}+bx+c=0$ are $x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$, then the roots of the quadratic equation ${{x}^{2}}-x-6=0$ are
$\begin{align}
  & \Rightarrow x=\dfrac{-\left( -1 \right)\pm \sqrt{{{\left( -1 \right)}^{2}}-4\left( 1 \right)\left( -6 \right)}}{2\left( 1 \right)} \\
 & \Rightarrow x=\dfrac{1\pm \sqrt{1+24}}{2} \\
 & \Rightarrow x=\dfrac{1\pm 5}{2} \\
 & \Rightarrow x=\dfrac{1+5}{2}\text{or }\dfrac{1-5}{2} \\
 & \Rightarrow x=3\text{ or }-2 \\
\end{align}$
Hence the roots of the given function are $x=-2,-2,1,3$. Here the multiplicity of $-2$ is $2$, $1$ is $1$ and $3$ is $1$. The graph of the given equation without roots will be

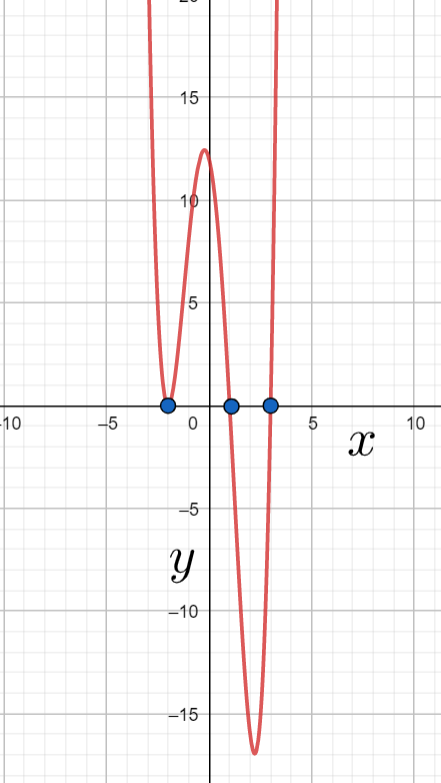
Same graph with the roots will be

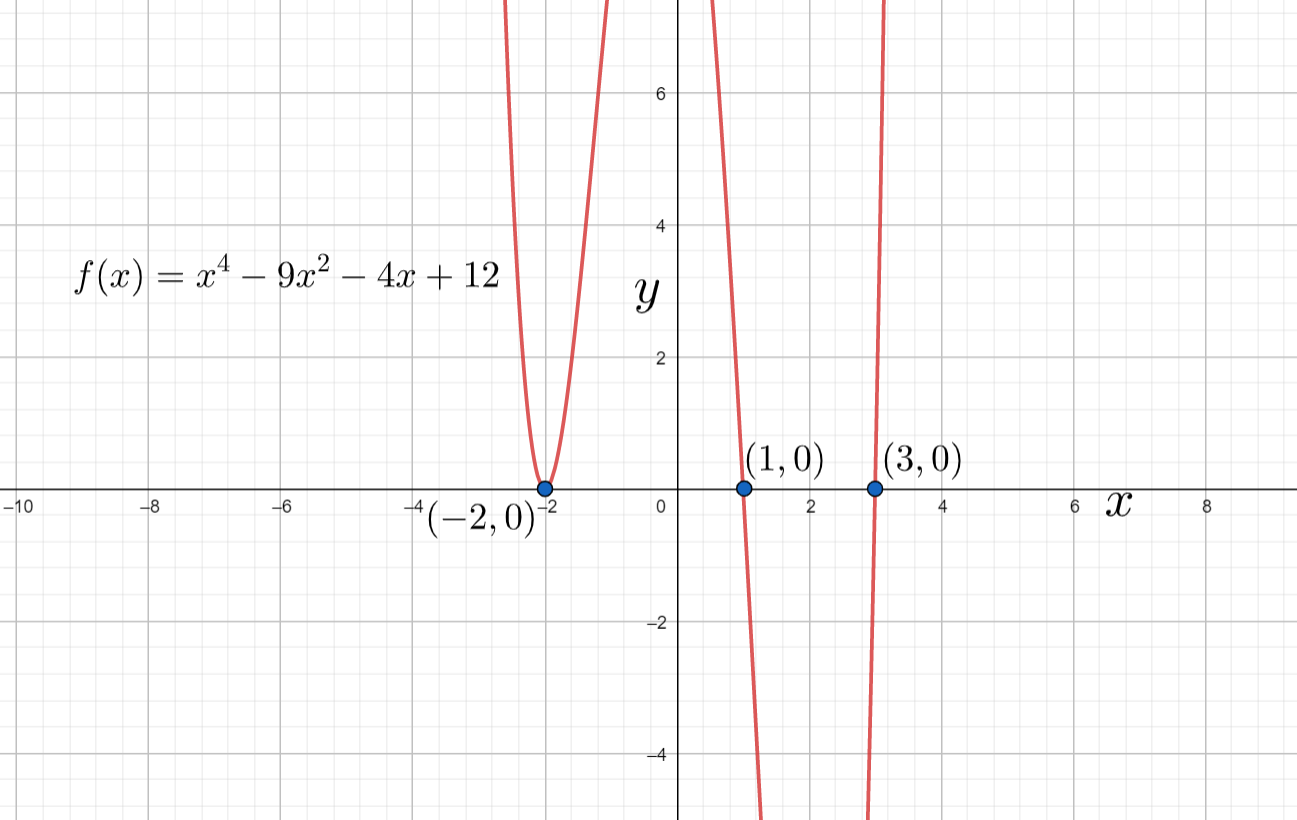
Note:
This problem seems to be lengthy so there may be chances of doing mistakes at any step. So, one should remember the process that we followed. We have first reduced the degree of the equation by one after calculating the one root value by dividing the given equation with the root.