
How do you find all zeros of $f\left( x \right)={{x}^{3}}-8{{x}^{2}}+25x-26$?
Answer
548.7k+ views
Hint: For this problem we need to find the zeros or roots of the given equation. We can observe that the given equation is a cubic equation. So, we will first check where the given function has zero value by substituting various $x$ values like $x=\pm 1,\pm 2,\pm 3,....$. After getting the one $x$ value, we will write that value as the root of the given equation. From this we will write the factor of the given equation and divide the given equation with the calculated factors. Now we will get a quadratic equation as result. We will use the quadratic equation formula to solve the quadratic equation to get the remaining two root values.
Complete step by step solution:
Given that, $f\left( x \right)={{x}^{3}}-8{{x}^{2}}+25x-26$.
Calculating the value of $f\left( 1 \right)$ by substituting $x=1$ in the above equation, then we will get
$\begin{align}
& \Rightarrow f\left( 1 \right)={{\left( 1 \right)}^{3}}-8{{\left( 1 \right)}^{2}}+25\left( 1 \right)-26 \\
& \Rightarrow f\left( 1 \right)=1-8+25-26 \\
& \Rightarrow f\left( 1 \right)=-8\ne 0 \\
\end{align}$
So $x=1$ is not a root of the given equation.
Now calculating the value of $f\left( -1 \right)$ by substituting $x=-1$ in the above equation, then we will get
$\begin{align}
& \Rightarrow f\left( -1 \right)={{\left( -1 \right)}^{3}}-8{{\left( -1 \right)}^{2}}+25\left( -1 \right)-26 \\
& \Rightarrow f\left( -1 \right)=-1-8-25-26 \\
& \Rightarrow f\left( -1 \right)=-60\ne 0 \\
\end{align}$
So $x=-1$ is not a root of the given equation.
Now calculating the value of $f\left( 2 \right)$ by substituting $x=2$ in the above equation, then we will get
$\begin{align}
& \Rightarrow f\left( 2 \right)={{\left( 2 \right)}^{3}}-8{{\left( 2 \right)}^{2}}+25\left( 2 \right)-26 \\
& \Rightarrow f\left( 2 \right)=8-32+50-26 \\
& \Rightarrow f\left( 2 \right)=0 \\
\end{align}$
So $x=2$ is the root of the given equation and $x-2=0$ is the factor of the given equation.
Now dividing the given equation with the factor $x-2=0$, then we will get
$\begin{align}
& 2\underline{\left| \begin{matrix}
\begin{matrix}
1 \\
0 \\
\end{matrix} & \begin{matrix}
-8 \\
\text{ } \text{ } 2 \\
\end{matrix} & \begin{matrix}
\text{ }25 \\
-12 \\
\end{matrix} & \begin{matrix}
-26 \\
\text{ } \text{ } \text{ }26 \\
\end{matrix} \\
\end{matrix} \right.} \\
& \text{ } \text{ } \text{ } \text{ } \text{ }1 \text{ } \text{ } \text{ } -6\text{ } \text{ } \text{ } \text{ } -13
\text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } 0 \\
\end{align}$From this we can write ${{x}^{3}}-8{{x}^{2}}+25x-26=\left( x-2 \right)\left( {{x}^{2}}-6x+13 \right)$.
Considering the quadratic equation ${{x}^{2}}-6x+13$.
The roots of the above quadratic equation from the quadratic formula are
$\Rightarrow x=\dfrac{-\left( -6 \right)\pm \sqrt{{{\left( -6 \right)}^{2}}-4\left( 1 \right)\left( 13 \right)}}{2\left( 1 \right)}$
Simplifying the above equation, then we will have
$\begin{align}
& \Rightarrow x=\dfrac{6\pm \sqrt{36-52}}{2} \\
& \Rightarrow x=\dfrac{6\pm \sqrt{-16}}{2} \\
\end{align}$
In the above equation we have the value $\sqrt{-16}$. We know that the square root of negative value is an imaginary number and the square root of $16$ is $4$. Substituting this value in the above equation, then we will get
$\begin{align}
& \Rightarrow x=\dfrac{6\pm 4i}{2} \\
& \Rightarrow x=\dfrac{6+4i}{2}\text{ or }\dfrac{6-4i}{2} \\
& \Rightarrow x=3+2i\text{ or }3-2i \\
\end{align}$
Hence the roots of the given equation are $x=2,3\pm 2i$. The graph of the given equation will be
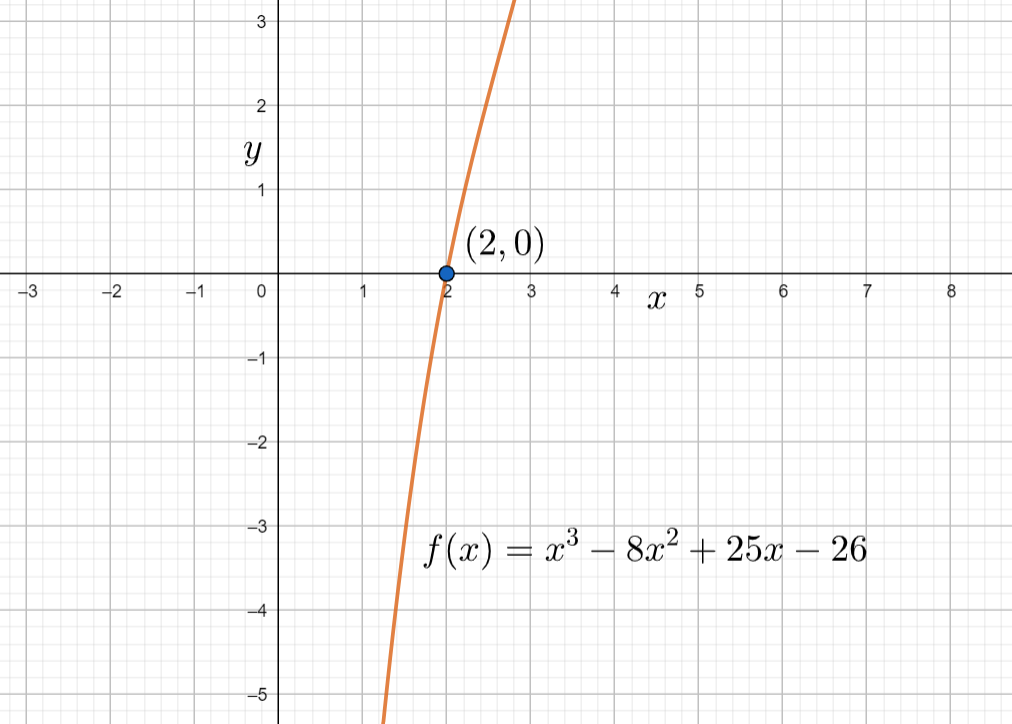
Note:
We can also check whether the calculated result is right or wrong by substituting the roots of the equation in the given equation. If the calculated roots satisfy the given equation, then our solution is correct otherwise we the solution is wrong.
Complete step by step solution:
Given that, $f\left( x \right)={{x}^{3}}-8{{x}^{2}}+25x-26$.
Calculating the value of $f\left( 1 \right)$ by substituting $x=1$ in the above equation, then we will get
$\begin{align}
& \Rightarrow f\left( 1 \right)={{\left( 1 \right)}^{3}}-8{{\left( 1 \right)}^{2}}+25\left( 1 \right)-26 \\
& \Rightarrow f\left( 1 \right)=1-8+25-26 \\
& \Rightarrow f\left( 1 \right)=-8\ne 0 \\
\end{align}$
So $x=1$ is not a root of the given equation.
Now calculating the value of $f\left( -1 \right)$ by substituting $x=-1$ in the above equation, then we will get
$\begin{align}
& \Rightarrow f\left( -1 \right)={{\left( -1 \right)}^{3}}-8{{\left( -1 \right)}^{2}}+25\left( -1 \right)-26 \\
& \Rightarrow f\left( -1 \right)=-1-8-25-26 \\
& \Rightarrow f\left( -1 \right)=-60\ne 0 \\
\end{align}$
So $x=-1$ is not a root of the given equation.
Now calculating the value of $f\left( 2 \right)$ by substituting $x=2$ in the above equation, then we will get
$\begin{align}
& \Rightarrow f\left( 2 \right)={{\left( 2 \right)}^{3}}-8{{\left( 2 \right)}^{2}}+25\left( 2 \right)-26 \\
& \Rightarrow f\left( 2 \right)=8-32+50-26 \\
& \Rightarrow f\left( 2 \right)=0 \\
\end{align}$
So $x=2$ is the root of the given equation and $x-2=0$ is the factor of the given equation.
Now dividing the given equation with the factor $x-2=0$, then we will get
$\begin{align}
& 2\underline{\left| \begin{matrix}
\begin{matrix}
1 \\
0 \\
\end{matrix} & \begin{matrix}
-8 \\
\text{ } \text{ } 2 \\
\end{matrix} & \begin{matrix}
\text{ }25 \\
-12 \\
\end{matrix} & \begin{matrix}
-26 \\
\text{ } \text{ } \text{ }26 \\
\end{matrix} \\
\end{matrix} \right.} \\
& \text{ } \text{ } \text{ } \text{ } \text{ }1 \text{ } \text{ } \text{ } -6\text{ } \text{ } \text{ } \text{ } -13
\text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } \text{ } 0 \\
\end{align}$From this we can write ${{x}^{3}}-8{{x}^{2}}+25x-26=\left( x-2 \right)\left( {{x}^{2}}-6x+13 \right)$.
Considering the quadratic equation ${{x}^{2}}-6x+13$.
The roots of the above quadratic equation from the quadratic formula are
$\Rightarrow x=\dfrac{-\left( -6 \right)\pm \sqrt{{{\left( -6 \right)}^{2}}-4\left( 1 \right)\left( 13 \right)}}{2\left( 1 \right)}$
Simplifying the above equation, then we will have
$\begin{align}
& \Rightarrow x=\dfrac{6\pm \sqrt{36-52}}{2} \\
& \Rightarrow x=\dfrac{6\pm \sqrt{-16}}{2} \\
\end{align}$
In the above equation we have the value $\sqrt{-16}$. We know that the square root of negative value is an imaginary number and the square root of $16$ is $4$. Substituting this value in the above equation, then we will get
$\begin{align}
& \Rightarrow x=\dfrac{6\pm 4i}{2} \\
& \Rightarrow x=\dfrac{6+4i}{2}\text{ or }\dfrac{6-4i}{2} \\
& \Rightarrow x=3+2i\text{ or }3-2i \\
\end{align}$
Hence the roots of the given equation are $x=2,3\pm 2i$. The graph of the given equation will be
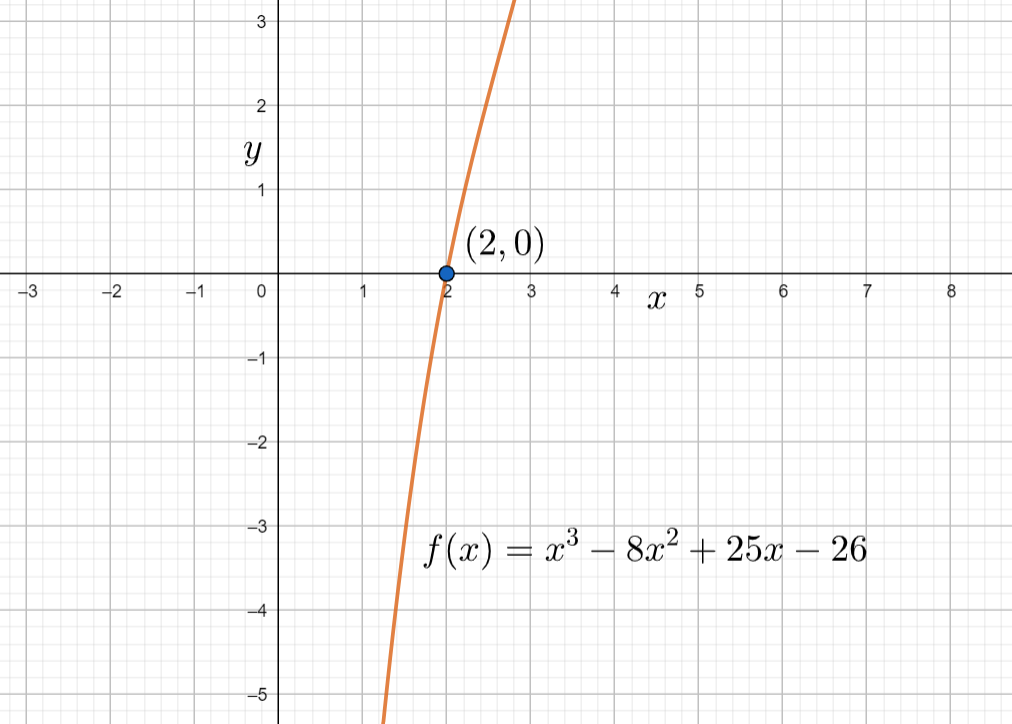
Note:
We can also check whether the calculated result is right or wrong by substituting the roots of the equation in the given equation. If the calculated roots satisfy the given equation, then our solution is correct otherwise we the solution is wrong.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The draft of the Preamble of the Indian Constitution class 10 social science CBSE

Who gave "Inqilab Zindabad" slogan?

Write a letter to the principal requesting him to grant class 10 english CBSE

Who was Subhash Chandra Bose Why was he called Net class 10 english CBSE




