Question

Find all the trigonometric ratios for the $\angle A$ given in the figure:

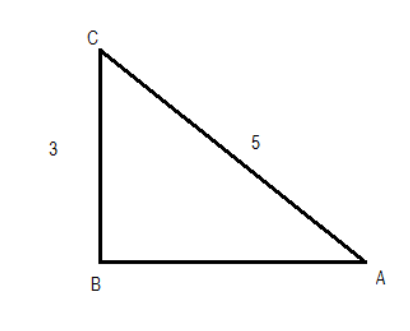
Answer 1

Hint: Start by finding the value of sinA using the basic definition that sine is the ratio of the perpendicular to the hypotenuse. Once you know the sign use the relation of sine with other trigonometric ratios to get the values of other trigonometric ratios.

Complete step-by-step answer:
Before moving to the solution, let us discuss the periodicity of sine and cosine function, and their relation with cosine and secant functions, which we would be using in the solution.
First, let us start with the graph of sinx and cosecx.

Next, let us see the graph of cosx and secx.

Now to start with the solution, we will find the value of sinA:
 $\sin A=\dfrac{perpendicular}{hypotenuse}=\dfrac{3}{5}$
Now we know that ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$ . So, we get
${{\sin }^{2}}A+{{\cos }^{2}}A=1$
 $\Rightarrow \dfrac{9}{25}+{{\cos }^{2}}A=1$
$\Rightarrow {{\cos }^{2}}A=\dfrac{16}{25}$
$\Rightarrow \cos A=\dfrac{4}{5}$
Now we also know that $\operatorname{tanA}=\dfrac{\operatorname{sinA}}{\cos A}$ . Therefore, the value of tanA is $\dfrac{3}{4}$ .
We also have that cotA is reciprocal of tanA. Hence the value of cotA is $\dfrac{4}{3}$ .
Similarly the values of secA and cosecA, being the reciprocals of cosA and sinA are is $\dfrac{5}{4}\text{ and }\dfrac{5}{3}$ , respectively.

Note: It is useful to remember the graph of the trigonometric ratios along with the signs of their values in different quadrants. For example: sine is always positive in the first and the second quadrant while negative in the other two.