Question

How do you find all the critical points to graph $9{{x}^{2}}-4{{y}^{2}}-90x-32y+125=0$ including vertices, foci and asymptotes?

Answer 1

Hint: Firstly, we need to use the completing the square method to obtain the given equation in the form of standard equation of a hyperbola which is given by $\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}-\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$. The coordinates of the centre are given as $\left( h,k \right)$. Since the hyperbola is horizontal, the coordinates of the vertices and the foci can be given as $\left( h\pm a \right)$ and $\left( h\pm c \right)$, where ${{c}^{2}}={{a}^{2}}+{{b}^{2}}$. Finally, the slopes of the asymptotes are given by $m=\pm \dfrac{b}{a}$ and the equations for the asymptotes can be determined using the point slope form.

Complete step by step solution:
The equation of the curve given in the question is
\[\Rightarrow 9{{x}^{2}}-4{{y}^{2}}-90x-32y+125=0\]
Arranging the x and the y terms together, we get
\[\Rightarrow 9{{x}^{2}}-90x-4{{y}^{2}}-32y+125=0\]
Now, we can take $9$ common from the first two terms and $-4$ from the next two terms to get
\[\Rightarrow 9\left( {{x}^{2}}-10x \right)-4\left( {{y}^{2}}+8y \right)+125=0\]
Multiplying and dividing the coefficients of x and y by $2$, we get
\[\begin{align}
  & \Rightarrow 9\left( {{x}^{2}}-10\times \dfrac{2}{2}x \right)-4\left( {{y}^{2}}+8\times \dfrac{2}{2}y \right)+125=0 \\
 & \Rightarrow 9\left( {{x}^{2}}-2\times 5\times x \right)-4\left( {{y}^{2}}+2\times 4\times y \right)+125=0 \\
\end{align}\]
Adding and subtracting \[{{5}^{2}}\] and \[{{4}^{2}}\] in the first and the second bracket respectively, we get
\[\begin{align}
  & \Rightarrow 9\left( {{x}^{2}}-2\times 5\times x+{{5}^{2}}-{{5}^{2}} \right)-4\left( {{y}^{2}}+2\times 4\times y+{{4}^{2}}-{{4}^{2}} \right)+125=0 \\
 & \Rightarrow 9\left( {{x}^{2}}-2\times 5\times x+{{5}^{2}}-25 \right)-4\left( {{y}^{2}}+2\times 4\times y+{{4}^{2}}-16 \right)+125=0 \\
 & \Rightarrow 9\left( {{x}^{2}}-2\times 5\times x+{{5}^{2}} \right)-9\left( 25 \right)-4\left( {{y}^{2}}+2\times 4\times y+{{4}^{2}} \right)-4\left( -16 \right)+125=0 \\
 & \Rightarrow 9\left( {{x}^{2}}-2\times 5\times x+{{5}^{2}} \right)-4\left( {{y}^{2}}+2\times 4\times y+{{4}^{2}} \right)-36=0 \\
\end{align}\]
Now, we can contract the first and the second brackets as
\[\begin{align}
  & \Rightarrow 9{{\left( x-5 \right)}^{2}}-4{{\left( y+4 \right)}^{2}}-36=0 \\
 & \Rightarrow 9{{\left( x-5 \right)}^{2}}-4{{\left( y+4 \right)}^{2}}=36 \\
\end{align}\]
Dividing both sides by \[36\], we get
\[\begin{align}
  & \Rightarrow \dfrac{9}{36}{{\left( x-5 \right)}^{2}}-\dfrac{4}{36}{{\left( y+4 \right)}^{2}}=1 \\
 & \Rightarrow \dfrac{{{\left( x-5 \right)}^{2}}}{4}-\dfrac{{{\left( y+4 \right)}^{2}}}{9}=1 \\
\end{align}\]
From the above equation, we can say that it is the equation of a hyperbola. Comparing it with the standard equation $\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}-\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$, we get
\[\begin{align}
  & \Rightarrow a=2 \\
 & \Rightarrow b=3 \\
\end{align}\]
Also,
$\begin{align}
  & \Rightarrow h=5 \\
 & \Rightarrow k=-4 \\
\end{align}$
This means that the centre of the hyperbola is at $\left( 5,-4 \right)$.
We know that c is related to a and b by
$\Rightarrow {{c}^{2}}={{a}^{2}}+{{b}^{2}}$
On substituting the values of a and b from above, we get
$\begin{align}
  & \Rightarrow {{c}^{2}}={{\left( 2 \right)}^{2}}+{{\left( 3 \right)}^{2}} \\
 & \Rightarrow {{c}^{2}}=4+9 \\
 & \Rightarrow {{c}^{2}}=13 \\
 & \Rightarrow c=\sqrt{13} \\
\end{align}$
Now, since the coefficient of ${{x}^{2}}$ is positive in the given equation, the axis of the hyperbola must be horizontal. This means that the y-coordinate of both the vertices and the foci must be equal to that of the center, that is $-4$.
Now, the x-coordinates of the vertices can be given by $\left( h\pm a \right)$. On substituting the above values, we get $\left( 5\pm 2 \right)$ and on solving we get $3$ and $7$. Therefore, the coordinates of the vertices are $\left( 3,-4 \right)$ and $\left( 7,-4 \right)$.
Also, the x-coordinates of the focus can be given by $\left( h\pm c \right)$. On substituting $h=5$ and $c=\sqrt{13}$, we get $\left( 5\pm \sqrt{13} \right)$. Therefore the coordinates of the foci are $\left( 5+\sqrt{13} \right)$ and $\left( 5-\sqrt{13} \right)$.
Finally, we know that the slopes of the asymptotes are given by
$\Rightarrow m=\pm \dfrac{b}{a}$
On substituting $a=2$ and $b=3$ we get
$\Rightarrow m=\pm \dfrac{3}{2}$
Since the asymptotes of a hyperbola pass through the centre, which in this case is at $\left( 5,-4 \right)$, from the point slope form we can write the equation of the asymptotes as
$\begin{align}
  & \Rightarrow \left( y-k \right)=m\left( x-h \right) \\
 & \Rightarrow \left( y+4 \right)=m\left( x-5 \right) \\
\end{align}$
On substituting $m=\dfrac{3}{2}$ we get
\[\Rightarrow y+4=\dfrac{3}{2}\left( x-5 \right)\]
Now, substituting $m=-\dfrac{3}{2}$ we get
\[\Rightarrow y+4=-\dfrac{3}{2}\left( x-5 \right)\]
We can observe these in the figure given below.

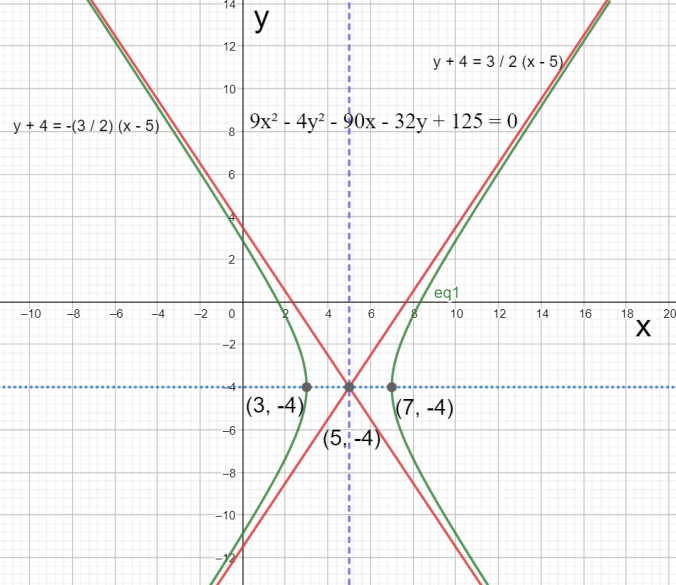
Hence, we have determined the centre, foci, vertices and the equations for the asymptotes for the given hyperbola.

Note: We must remember all of the important results for the hyperbola $\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}-\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1$, which are used in the above solution. We must not get confused between the relations ${{c}^{2}}={{a}^{2}}+{{b}^{2}}$ and ${{c}^{2}}={{a}^{2}}-{{b}^{2}}$. The former is valid for a hyperbola while the latter is valid for an ellipse.