Question

How do you find all real and complex roots of $2{{x}^{4}}+3{{x}^{3}}-{{x}^{2}}+5=0$ ?

Answer 1

Hint: We are given a polynomial equation of 4-degree. This implies that this equation has 4 roots. However, all of these might not be real roots and rather would be complex roots. Therefore, we will use Descartes's method to find all the roots of the given equation. Using this method, we will do simple comparing of coefficients of like terms and solve them further.

Complete step-by-step solution:
The Descartes’ method involves assuming the biquadratic equation as the product of two quadratic equations which can be then compared to the coefficients of the actual equation.
Given the polynomial function, $2{{x}^{4}}+3{{x}^{3}}-{{x}^{2}}+5=0$.

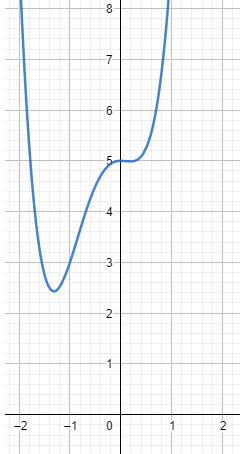
Looking at the graph of the function, we understand that the function does not have any real roots as it is not cutting through the x-axis even once.
For $2{{x}^{4}}+3{{x}^{3}}-{{x}^{2}}+5=0$, we have only unreal roots which would occur in conjugate pairs.
Let $2{{x}^{4}}+3{{x}^{3}}-{{x}^{2}}+5=\left( a{{x}^{2}}+bx+c \right)\left( d{{x}^{2}}+ex+f \right)$
Thus on solving, we get
$a=2,b=\sqrt{\dfrac{11}{5}},c=1,d=1,e=-\sqrt{55},f=5$
$\begin{align}
  & \Rightarrow 2{{x}^{4}}+3{{x}^{3}}-{{x}^{2}}+5=\left( 2{{x}^{2}}+\sqrt{\dfrac{11}{5}}x+1 \right)\left( 1.{{x}^{2}}-\sqrt{55}x+5 \right) \\
 & \Rightarrow 2{{x}^{4}}+3{{x}^{3}}-{{x}^{2}}+5=\left( 2{{x}^{2}}+\sqrt{\dfrac{11}{5}}x+1 \right)\left( {{x}^{2}}-\sqrt{55}x+5 \right) \\
\end{align}$
The roots of these quadratics are the roots of the given 4-degree polynomial given as $x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$.
Roots of $2{{x}^{2}}+\sqrt{\dfrac{11}{5}}x+1$:
$x=\dfrac{-\sqrt{\dfrac{11}{5}}\pm \sqrt{{{\left( \sqrt{\dfrac{11}{5}} \right)}^{2}}-4\left( 2 \right)\left( 1 \right)}}{2\left( 2 \right)}$
$\begin{align}
  & \Rightarrow x=\dfrac{-\sqrt{\dfrac{11}{5}}\pm \sqrt{\dfrac{11}{5}-8}}{4} \\
 & \Rightarrow x=\dfrac{-\sqrt{\dfrac{11}{5}}\pm \sqrt{\dfrac{-29}{5}}}{4} \\
\end{align}$
We shall replace the negative one under the root by iota.
$\Rightarrow x=\dfrac{-\sqrt{11}\pm i \sqrt{29}}{4\sqrt{5}}$
Thus the roots of $2{{x}^{2}}+\sqrt{\dfrac{11}{5}}x+1$ are $\dfrac{-\sqrt{11}+\iota \sqrt{29}}{4\sqrt{5}},\dfrac{-\sqrt{11}-\iota \sqrt{29}}{4\sqrt{5}}$.
Now, the roots of ${{x}^{2}}-\sqrt{55}x+5$.
 $x=\dfrac{-\left( -\sqrt{55} \right)\pm \sqrt{{{\left( -\sqrt{55} \right)}^{2}}-4\left( 1 \right)\left( 5 \right)}}{2\left( 1 \right)}$
$\begin{align}
  & \Rightarrow x=\dfrac{\sqrt{55}\pm \sqrt{55-20}}{2} \\
 & \Rightarrow x=\dfrac{\sqrt{55}\pm \sqrt{35}}{2} \\
\end{align}$
Thus the roots of ${{x}^{2}}-\sqrt{55}x+5$ are $\dfrac{\sqrt{55}+\sqrt{35}}{2},\dfrac{\sqrt{55}-\sqrt{35}}{2}$.
Therefore, all real and complex roots of $2{{x}^{4}}+3{{x}^{3}}-{{x}^{2}}+5=0$are $\dfrac{-\sqrt{11}+\iota \sqrt{29}}{4\sqrt{5}},\dfrac{-\sqrt{11}-\iota \sqrt{29}}{4\sqrt{5}}$and $\dfrac{\sqrt{55}+\sqrt{35}}{2},\dfrac{\sqrt{55}-\sqrt{35}}{2}$.

Note: The non-real, complex roots come in conjugate pairs. This means that there can never be one non-real or complex, rather non-real roots will always occur in the number of 2 or multiples of 2. Another method of locating the roots is by sketching the graph and then seeing where the graph meets the y-axis.