Question

Find a point corresponding to $3+\sqrt{2}$ on the number line.

Answer 1

Hint: First we must represent the rational part, that is, 3. And after that, we can use the Pythagoras theorem to represent the irrational part, which is, $\sqrt{2}$. Then, with the help of a compass, we can draw an arc with radius as $\sqrt{2}$ and mark the point on the number line. This will be the required point.

Complete step by step answer:
We know that any number that can be expressed in the form $\dfrac{p}{q}$, where p and q are integers and q is not equal to 0, is called a rational number. And any number that is not rational is called an irrational number.
Here, we can see that there is no possible way to express $\sqrt{2}$ in the form $\dfrac{p}{q}$, where p and q are integers and q is not equal to 0. Thus, we can clearly say that $\sqrt{2}$ is an irrational number.
We also know that all irrational numbers in decimal form are of the form non terminating and non repeating. Hence, we cannot represent $\sqrt{2}$ on the number line directly, like we represent other decimal values. So, we must find an alternative method to plot the value $\sqrt{2}$.
In this question, we need to represent $3+\sqrt{2}$ on the number line. Let us first represent 3 on the number line.

Now, we can use the well known Pythagoras theorem to draw the distance $\sqrt{2}$.
Let us assume a right angled triangle with base = 1 unit and height = 1 unit. Then by Pythagoras theorem, we can say that
${{\left( \text{Hypotenuse} \right)}^{2}}={{1}^{2}}+{{1}^{2}}$
And, so the length of hypotenuse is
Hypotenuse = $\sqrt{2}$

Now, we can draw an arc with centre at 3 and radius equal to $\sqrt{2}$.

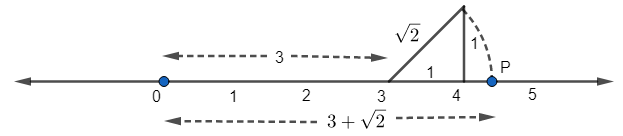
The point P represents $3+\sqrt{2}$ on the number line.

Note: We must remember that all real numbers, either rational or irrational, can be plotted on the number line. Also, we cannot represent the irrational numbers directly on the number line, like we do in case of rational numbers.