
How do I find a perpendicular line to a vertical line graph e.g. \[x=2\] ?
Answer
532.2k+ views
Hint: This particular problem can be solved comfortably with a fair idea and knowledge of coordinate geometry and straight lines. In general, to find the equation of a straight line which is perpendicular to another straight line, we first need to find the slope of the straight line using the formula \[{{m}_{1}}\times {{m}_{2}}=-1\] . After this we can easily find the equation using the point slope method. However, this problem can be done in a much simpler way which is by observing the different scenarios of the sum.
Complete step by step solution:
Now, we start off with the solution to the given problem by writing that the line represented in the given problem by \[x=2\] is a line which is parallel to the y-axis and is perpendicular to the x-axis. Since we know that the x-axis and the y-axis are perpendicular to one another, solving this problem becomes much easier.
Since the given line is parallel to the y-axis and perpendicular to the x-axis, thus the line which will be perpendicular to this line will be parallel to the x-axis and perpendicular to the y-axis. There can be any line of this description. Hence, we can generalize the statement and say that,
\[y=c\] , where \[c\] is any constant, is the line which is perpendicular to the line \[x=2\]
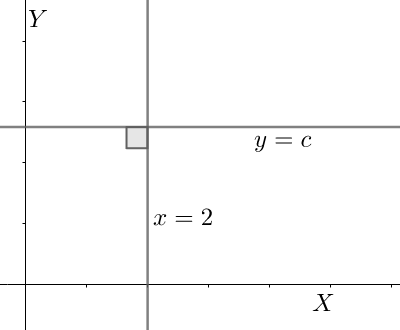
Note: These types of problems are very easy to solve once we know the core concepts of coordinate geometry. However, this problem can also be done using another technique, which is by graphs. We plot the graph for \[x=2\] and then we can easily predict what shall be the graph for its perpendicular line, or we may use a protractor to draw one for easier understanding. We must be very careful while finding the perpendicular of any line as they are prone to mistakes like, finding the wrong value of slope, putting the wrong point on the equation and many more.
Complete step by step solution:
Now, we start off with the solution to the given problem by writing that the line represented in the given problem by \[x=2\] is a line which is parallel to the y-axis and is perpendicular to the x-axis. Since we know that the x-axis and the y-axis are perpendicular to one another, solving this problem becomes much easier.
Since the given line is parallel to the y-axis and perpendicular to the x-axis, thus the line which will be perpendicular to this line will be parallel to the x-axis and perpendicular to the y-axis. There can be any line of this description. Hence, we can generalize the statement and say that,
\[y=c\] , where \[c\] is any constant, is the line which is perpendicular to the line \[x=2\]
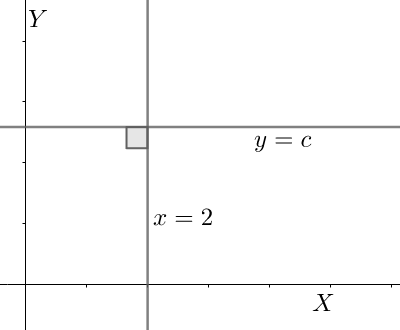
Note: These types of problems are very easy to solve once we know the core concepts of coordinate geometry. However, this problem can also be done using another technique, which is by graphs. We plot the graph for \[x=2\] and then we can easily predict what shall be the graph for its perpendicular line, or we may use a protractor to draw one for easier understanding. We must be very careful while finding the perpendicular of any line as they are prone to mistakes like, finding the wrong value of slope, putting the wrong point on the equation and many more.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE




