
How do you find a parametric equation for a given curve ${y^2} = 4ax$?
Answer
495.3k+ views
Hint: As this curve is present in the x-y plane we can choose one coordinate in terms of variables and then find the second coordinate by putting it in the equation of parabola. The x and y coordinates we get are the equation of the parabola in terms of the new parameter.
Complete step by step solution:
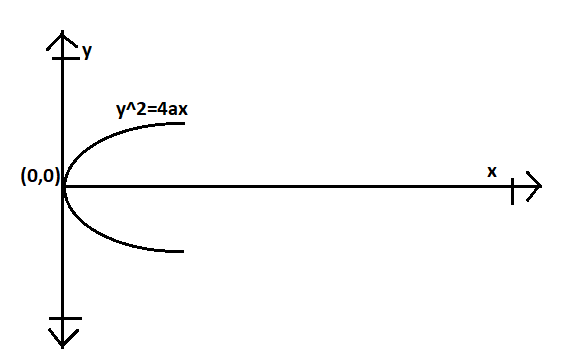
In the given question, we have
Equation of parabola is ${y^2} = \,4ax$
Also,
The given equation is in the xy- plane. It is a parabola with horizontal axis of symmetry and vertex in the origin.
As we know that,
The value of x and y are the coordinates in the xy plane.
The parabola gives the direct relation between x and y. Each and every point of the parabola must satisfy this relation. Also, parametric equations represent each point of the parabola as a function of the parameter of ‘t’.
Let, $x = a{t^2}$
Here we have chosen this value of x in terms of t because we will get a simplified value of y after putting this in the equation.
Therefore, put the above value of x in the parabola equation.
${y^2} = \,4a\left( {a{t^2}} \right)$
${y^2} = 4{a^2}{t^2}$
Taking root both sides
$y = 2at$
Therefore, the equation of parabola is $x = a{t^2}$and $y = 2at$ for every $t\, \in R$.
Note: Basically, there are two types of parabolas one with axis as x-axis and the other one with as y- axis. This one is with an axis as x-axis. Also, there can be parabolas whose vertex may not be the origin.
Then, their parametric equation would be different from this one.
Complete step by step solution:
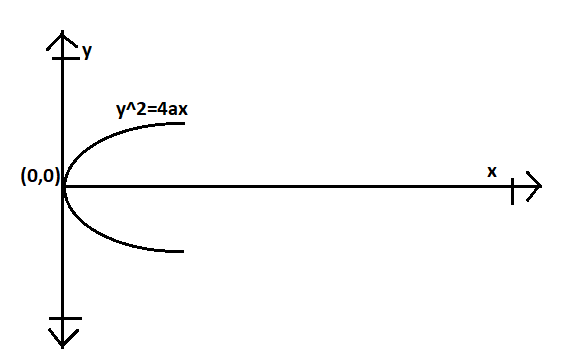
In the given question, we have
Equation of parabola is ${y^2} = \,4ax$
Also,
The given equation is in the xy- plane. It is a parabola with horizontal axis of symmetry and vertex in the origin.
As we know that,
The value of x and y are the coordinates in the xy plane.
The parabola gives the direct relation between x and y. Each and every point of the parabola must satisfy this relation. Also, parametric equations represent each point of the parabola as a function of the parameter of ‘t’.
Let, $x = a{t^2}$
Here we have chosen this value of x in terms of t because we will get a simplified value of y after putting this in the equation.
Therefore, put the above value of x in the parabola equation.
${y^2} = \,4a\left( {a{t^2}} \right)$
${y^2} = 4{a^2}{t^2}$
Taking root both sides
$y = 2at$
Therefore, the equation of parabola is $x = a{t^2}$and $y = 2at$ for every $t\, \in R$.
Note: Basically, there are two types of parabolas one with axis as x-axis and the other one with as y- axis. This one is with an axis as x-axis. Also, there can be parabolas whose vertex may not be the origin.
Then, their parametric equation would be different from this one.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




