Question

Find a number that is divisible by 15, 18 and 25 and is a perfect square.
1) 225
2) 450
3) 400
4) 900

Answer 1

Hint: We will first find the LCM of the given numbers, 15,18 and 25. Then we will check whether the number is a perfect square or not. If the resultant number is not a perfect square, then take a multiple of it, which is a perfect square.

Complete step-by-step answer:
Here, we start the question by finding the LCM of 15,18 and 25.
LCM of 15,18 and 25 will give us the smallest common multiple of these numbers. Hence, that number will be divisible by all the given numbers.
Let us first write the factors of each given number.
The factors of 15 are $3 \times 5$
The factors of 18 are $2 \times 3 \times 3$
Similarly, the factors of 25 are $5 \times 5$.
Next, write the LCM of the three numbers using their factors.
LCM is calculated by multiplying each factor the maximum number of times it comes in each given number.
That is, LCM of 15,18 and 25 is
$2 \times 3 \times 3 \times 5 \times 5$
This can also be written as,
$2 \times {3^2} \times {5^2}$
The above number will not make a perfect square as 2 is not multiplied with itself.
But, we want to find the number which is a perfect square.
Hence, multiply the number by 2.
Then, we will get,
${2^2} \times {3^2} \times {5^2} = 900$,which is a perfect square
Thus, 900 is divisible by 15,18 and 25 and is perfect square.
Hence, option D is the correct answer.

Note:- For finding the LCM, we can also use the common division method.

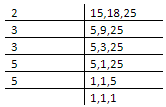
Hence, the LCM of 15,18 and 25 is $2 \times {3^2} \times {5^2}$
Also, a perfect square is those numbers which are the product of the same integers.