Question

Find \[A \cup B\]and \[A \cap B\]if \[A = \{ 2,6,10,14\} \],\[B = \{ 2,5,14,16\} \].

Answer 1

Hint: The question requires to find union and intersection of the given set by using set theory. Sets are an ordered array of items in mathematics that can be expressed in set-builder or roster form. Curly braces \[\{ \} \] are often used to display sets.

Complete step-by-step answer:
We are the given \[A = \{ 2,6,10,14\} \],\[B = \{ 2,5,14,16\} \] then
Finding \[A \cup B\]:
In set theory, the set of all elements in a series of sets is called the union. It is a fundamental operation that allows sets to be combined and compared to one another.
Union of Set \[A\]and \[B\]contains all the elements of both \[A\]and \[B\]. It is denoted as \[A \cup B\].
In the given question, \[A \cup B\]can be found out as follows:
\[ \Rightarrow A \cup B = \{ 2,6,10,14\} \cup \{ 2,5,14,16\} \]
Write all the terms without repeating the common terms. Hence, we will get:
\[ \Rightarrow A \cup B = \{ 2,5,6,10,14,16\} \]
Finding \[A \cap B\]:
In set theory, intersection of set contains all the common elements of the given set.
Intersection of Set\[A\]and \[B\]contains all the elements which belong to both Set \[A\]and \[B\].It is denoted as\[A \cap B\].
In the given question, \[A \cap B\]can be found out as follows:
\[ \Rightarrow A \cap B = \{ 2,6,10,14\} \cap \{ 2,5,14,16\} \]
Writing the common term in both the sets, we get,
\[ \Rightarrow A \cap B = \{ 2,14\} \]


Hence \[A \cup B = \{ 2,5,6,10,14,16\} \] and \[A \cap B = \{ 2,14\} \].

Note: When two or more sets combine to form a single set under any of the specified conditions, set theory operations are carried out. The basic set operations are union, intersection, complement of set, cartesian products of set and set difference.
Union and Intersection of set can also be easily found out with the help of Venn diagram. A Venn diagram is a diagram that uses circles to depict relationships between objects or finite groups of objects. The Venn Diagram of given sum can be drawn as:

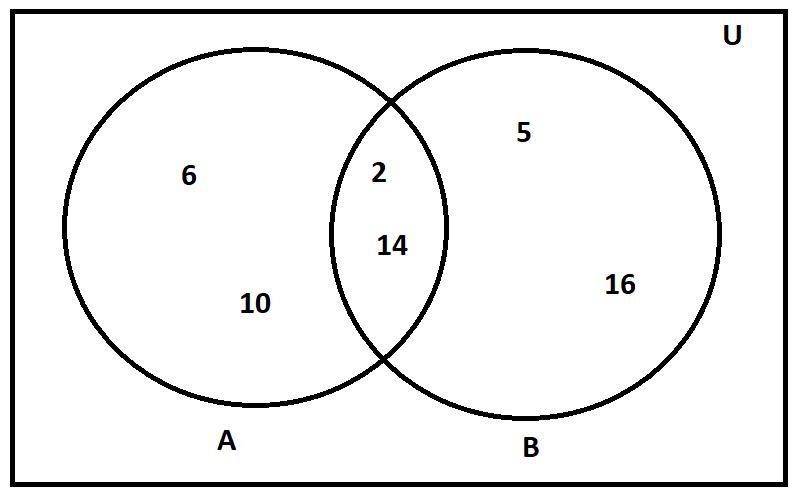
\[A \cup B = \{ 2,5,6,10,14,16\} \]and \[A \cap B = \{ 2,14\} \]can be easily found out from the Venn diagram.