Question

Find 4 integers that are less than \[ - 10\].

Answer 1

Hint:
We can find integers less than \[ - 10\] by subtracting any positive integers from it. Subtract first positive integer to find the first integer less than \[ - 10\], subtract the second positive integer to find the second integer less than \[ - 10\] and so on. We can also find integers less than \[ - 10\] by plotting a number line and looking for integers on the left side of \[ - 10\].

Complete step by step solution:
We can subtract any 4 positive integers from \[ - 10\] to obtain integers that are less than \[ - 10\]. Let us choose 1, 2, 3 and 4 as 4 positive integers.
First, let us subtract 1 from \[ - 10\]:
\[ - 10 - 1 = - 11\]
We have obtained \[ - 11\] as the first integer which is less than \[ - 10\].
Then, let us subtract 2 from \[ - 10\]:
\[ - 10 - 2 = - 12\]
We have obtained \[ - 12\] as the second integer which is less than \[ - 10\].
Similarly, let us subtract 3 from \[ - 10\]:
\[ - 10 - 3 = - 13\]
We have obtained \[ - 13\] as the third integer which is less than \[ - 10\].
Finally, let us subtract 4 from \[ - 10\]:
\[ - 10 - 4 = - 14\]
We have obtained \[ - 14\] as the fourth integer which is less than \[ - 10\].

So, 4 integers that are less than \[ - 10\] are \[ - 11\], \[ - 12\], \[ - 13\] and \[ - 14\].

Note:
For any negative integer, the numbers that are smaller in magnitude are not less than the number. For example, \[ - 9\] is not smaller than \[ - 10\], it is larger than \[ - 10\].
Alternatively, we can also solve the question by using a number line. On a number line, the integers to the right of a given number are greater than it and the integers to the left of a given number are less than it.
First, we will plot a number line. Then, we will mark the integer \[ - 10\] on it. Now, we will look for integers on the left side of \[ - 10\].

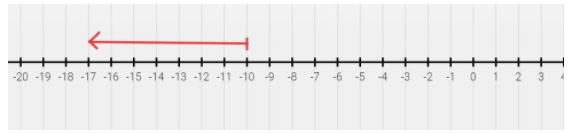
 In the given figure, all the integers that are on the left side of \[ - 10\] are less than it. They are represented by a red arrow pointing towards the left. Some of the integers are \[ - 11\], \[ - 12\], \[ - 13\], \[ - 14\], \[ - 15\], \[ - 16\], \[ - 17\], \[ - 18\], \[ - 19\] and \[ - 20\].
There are infinite integers that are less than \[ - 10\] because we know that the number line extends indefinitely on both sides.