Question

Fill the blanks in the following equation
     \[~~~A-\text{ }(B\cup C\cup D)\text{ }=\text{ }\left( A-B \right)\cap \ldots .\cap \ldots ..\]

Answer 1

Hint: As we know that the Venn diagram for four sets is so complicated we are going to check what the answer will be when we take it as two and three sets and then we can get the answer for four sets. Check first for 2 sets and then check for three sets using the Venn diagram.

 Complete step by step answer:
So let us first take two sets i.e. A and B ;
Which implies the question will be A-B and this is equal to A-B which is the same.
Now coming to the next three sets i.e. A, B, C ;
Which implies the question will be \[A-\text{ }(B\cup C)\text{ }=\text{ }\left( A-B \right)\cap \ldots .\]
Now we will find what the value of the question is.. using a Venn diagram for 3 sets.

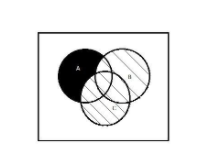
The above diagram is a Venn diagram of 3 sets A, B, C.
We know that the part with lines is \[(B\cup C)\] which implies the shaded part(that is the region that is painted with dark black color ) will be \[A-\text{ }(B\cup C)\]
It can be clearly told that the shaded part will also be equal to intersection of (A-C) and (A-B)
which implies \[A-\text{ }(B\cup C)\text{ }=\text{ }\left( A-B \right)\cap \left( A-C \right)\]
From this iteration we can easily say that for four sets \[A-\text{ }(B\cup C\cup \text{ }D)\text{ }=\text{ }\left( A-B \right)\cap \left( A-C \right)\cap \left( A-D \right)\]
So the terms that are to be filled in the question are \[\left( A-C \right)\text{ }and\text{ }\left( A-D \right).\]

Note:
While solving questions involving intersection and union of sets it is always better to solve it using a venn diagram representing the sets. Questions of this kind can also be solved using direct usage of laws of sets but it might make the problem lengthier to solve. $A-\left( B\cap C \right)$ represents the space that excludes intersection of B and C from A.