Question

Fill in the blanks:
A brick has ______ faces and _____ edges.

Answer 1

Hint: We solve this problem by using the definition of face and edge of a 3D figure.
We use the condition that brick is an example of cuboid.
We have the definition of face as the flat or a curved surface of a 3D object
We have the definition of edge is the line segment where two faces meet.

Complete answer:
We are asked to find the number of faces and edges of a brick
We know that the brick is an example of cuboid.
Let us take the rough figure of a cuboid as follows

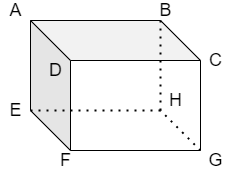
Now, let us find the number of faces and edges of above cuboid
We know that the definition of face as the flat or a curved surface of a 3D object
Here, we can see that all the surfaces are flat.
Now, let us make a list of surfaces in the above cuboid as follows
(1) ABCD
(2) DCGF
(3) EFGH
(4) ABEH
(5) ADEF
(6) BCGH
Here, we can see that there are total of 6 faces for a cuboid
Now, let us find the number of edges of the cuboid
We know that the definition of edge is the line segment where two faces meet.
Now, let us make a list of edges in the above cuboid then we get
(1) AB
(2) BC
(3) CD
(4) DA
(5) EF
(6) FG
(7) GH
(8) HE
(9) AE
(10) DF
(11) BH
(12) CG
Here, we can see that there are total of 12 edges
Therefore we can conclude that there are a total of 6 faces and 12 edges for brick.

Note:
Students may make mistakes in finding the number of edges.
We have the number of edges is the intersection of two faces
Here, we can see that the selection of two faces from 6 faces gives the number of edges.
We know that selection of \[r\] objects from \[n\] objects is given as \[{}^{n}{{C}_{r}}\]
By using the above condition we get the number of edges as
\[\begin{align}
  & \Rightarrow {}^{6}{{C}_{2}}=\dfrac{6!}{2!\left( 6-4 \right)!} \\
 & \Rightarrow {}^{6}{{C}_{2}}=\dfrac{6\times 5}{2}=15 \\
\end{align}\]
Here, we can see that it was 15 because there are some edges that are repeated in this process.
Also, we cannot tell how many repeated also.
So, we cannot follow this process as it gives the wrong answer.