Question

Fill in the blank:
The total surface area of the cube is _____
A. \[3{a^2}\]
B. \[6{a^2}\]
C. \[4{a^2}\]
D. \[5{a^2}\]

Answer 1

Hint: We use the number of faces of a cube and the fact that the cube has all its sides of equal length. Each face of a cube is of the shape of a square and we know the area of a square is side square. Calculate area of one face and multiply with number of faces of the surface.
* If we have a square having length of side as ‘a’ units then its area is \[{a^2}\] square units.

Complete step-by-step solution:
We draw a rough diagram of a cube of length of side ‘a’ units.
 

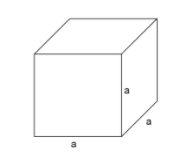
Since we know each face of a cube is a square of length of side ‘a’ units, then we can calculate the area of one square face of the cube.
\[ \Rightarrow \]Area of one face of cube \[ = {a^2}\]square units
Now we calculate the number of faces that are there on the total surface. Since we know the total surface area is the area covered by the surface of the figure then we can count there are 6 such square faces of the cube.
Use a unitary method to calculate the area of 6 such square faces of a cube.
Since 1 square face has area \[{a^2}\]square units
 \[ \Rightarrow \]Area of 6 square faces \[ = 6{a^2}\]square units.
Since all 6 square faces completely cover the surface of the cube, we can say the total surface area of the cube is \[6{a^2}\]square units.

\[\therefore \]Option B is correct.

Note: Many students make the mistake of excluding one of the square faces of the cube as they think it won’t be included in the total surface area because it is joined or facing towards the ground i.e. it is the face that is not as a surface. Keep in mind total surface area is the total area that the figure has on the outside.