Question

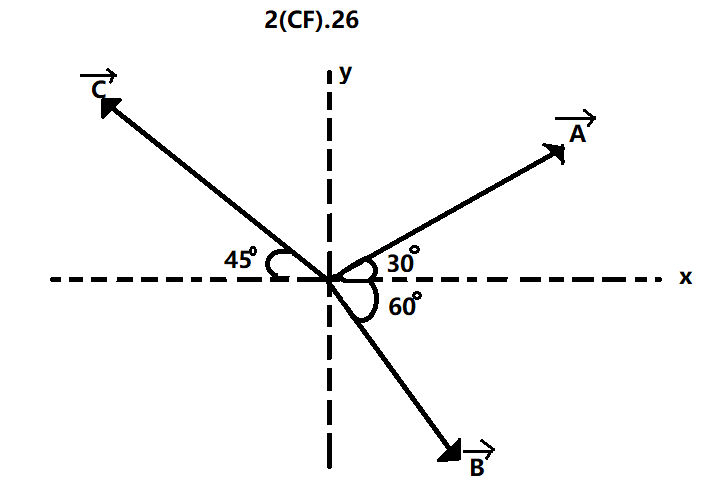
Figure shows three vectors \[\overrightarrow {OA,} \overrightarrow {OB} ,\overrightarrow {OC} \] having the same magnitude. The direction of \[\overrightarrow {OA} + \overrightarrow {OB} - \overrightarrow {OC} \], With X-axis is

(a) \[{\tan ^{ - 1}}\left( {\dfrac{{2 - \sqrt 3 - 1}}{{2 + \sqrt 3 + 1}}} \right)\]
(b) \[{\tan ^{ - 1}}\left( {\dfrac{{1 - \sqrt 3 - \sqrt 2 }}{{1 + \sqrt 3 + \sqrt 2 }}} \right)\]
(c) \[{\tan ^{ - 1}}\left( {\dfrac{{1 - \sqrt 3 + \sqrt 2 }}{{1 - \sqrt 3 - \sqrt 2 }}} \right)\]
(d) \[{\tan ^{ - 1}}\left( {\dfrac{{1 + \sqrt 3 + \sqrt 2 }}{{1 - \sqrt 3 + \sqrt 2 }}} \right)\]

Answer 1

Hint: We are given three vectors \[\overrightarrow {OA,} \overrightarrow {OB} ,\overrightarrow {OC} \] having the same magnitude.
We have to find out the direction of \[\overrightarrow {OA} + \overrightarrow {OB} - \overrightarrow {OC} \], the x-axis. The magnitude of a vector is nothing only its length.
The scaler x component of a vector can be expressed as a product of its magnitude with the cosine of its direction angle. The scaler y component can be expressed as a product of the magnitude of its direction angle.

Complete answer:
 Let us assume that,
\[|\overrightarrow {OA|} = |\overrightarrow {OB|} = |\overrightarrow {OC|} \] [Given in question that magnitude of three vectors is same]
Now,
\[|\overrightarrow {OA|} \] is in \[xy\] range so,
\[\overrightarrow {OA} = A\cos {30^ \circ }\widehat i + A\sin {30^ \circ }\]
\[\overrightarrow {OB} = A\cos {60^ \circ }\widehat i - A\sin {60^ \circ }\widehat j\] [ y range is negative]
\[\overrightarrow {OC} = - A\cos {45^ \circ }\widehat i + A\sin {45^ \circ }\widehat j\][x range is negative]
Now putting the value of trigonometric angles,
\[\overrightarrow {OA} = \dfrac{{\sqrt {3A} }}{2}\widehat i + \dfrac{A}{2}\widehat j\]
\[\overrightarrow {OB} = \dfrac{A}{2}\widehat i - \dfrac{{\sqrt {3A} }}{2}\widehat j\]
\[\overrightarrow {OC} = \dfrac{{ - A}}{2}\widehat i + \dfrac{A}{{\sqrt 2 }}\widehat j\]
Now we have to find the direction of \[\overrightarrow {OA} + \overrightarrow {OB} - \overrightarrow {OC} \]
So,
\[\left( {\dfrac{{\sqrt {3A} }}{2} + \dfrac{A}{2} + \dfrac{A}{{\sqrt 2 }}} \right)\widehat i + \left( {\dfrac{A}{2} - \dfrac{{\sqrt {3A} }}{2} + \dfrac{A}{2}} \right)\widehat j\]
Taking out \[\dfrac{A}{2}\] Common we get
\[\dfrac{A}{2}\left( {\sqrt 3 + 1 + \sqrt 2 } \right)\widehat i + \dfrac{A}{2}\left( {1 - \sqrt 3 + \sqrt 2 } \right)j\]
Now to find the direction of the three vectors we are going to use the formula
\[\tan \theta = \dfrac{{y\ component}}{{x\ component}}\]
=\[\dfrac{{\dfrac{A}{2}\left( {1 - \sqrt 3 + \sqrt 2 } \right)}}{{\dfrac{A}{2}\left( {\sqrt 3 + 1 + \sqrt 2 } \right)}}\]
=\[\dfrac{{\left( {1 - \sqrt 3 - \sqrt 2 } \right)}}{{\left( {\sqrt 3 + 1 + \sqrt 2 } \right)}}\]
\[\theta = {\tan ^{ - 1}}\dfrac{{\left( {1 + \sqrt 3 + \sqrt 2 } \right)}}{{\left( {1 - \sqrt 3 + \sqrt 2 } \right)}}\]
So, the direction of the three vectors is\[\theta = {\tan ^{ - 1}}\dfrac{{\left( {1 + \sqrt 3 + \sqrt 2 } \right)}}{{\left( {1 - \sqrt 3 + \sqrt 2 } \right)}}\]
Therefore option (d) is the correct answer for the given question.

Therefore, the correct option is A

Note: It is the fact that the vector sum of two or more vectors is known as the 'resultant vector' and it is the result of adding two or more vectors together.
Also, the tangent of an angle is the trigonometric ratio of the adjacent and opposite sides of a right-angle triangle comprising the angle.
In the question the first three options are not obtained during calculation therefore those options are incorrect for these questions. Also, while defining the magnitude of vectors the sign of quadrant should be taken care of as this can hurdle the solution.