Question

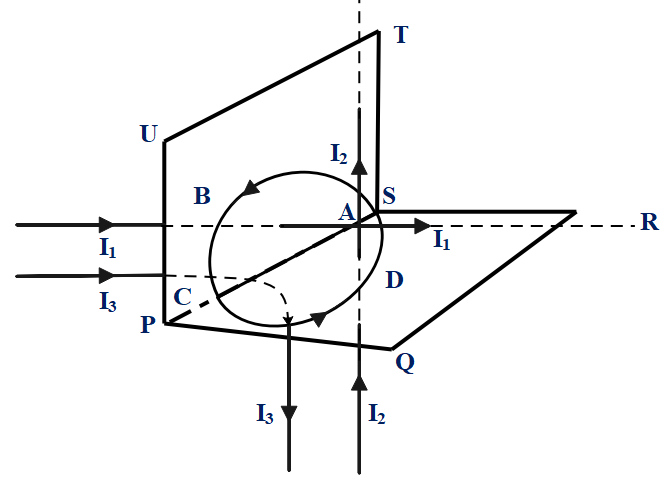
Figure shows an Amperian path ABCDA. Part ABC is in vertical plane PSTU while part CDA is in horizontal plane PQRS. Direction of circulation along the path is shown by an arrow near point B and D.
 $\oint{\vec{B}.d\vec{l}}$ for this path along according to Ampere’s law will be:

Answer 1

Hint: We know that an electricity and magnetism are inter connected. We also know that a current carrying conductor produces magnetic field in its surrounding and similarly, a changing magnetic field induces current in the coil.
Formula:
$\mu_{0}I=\oint{\vec{B}.d\vec{l}}$

Complete answer:
We know from ampere's law that the magnetic field is produced due to a current that is independent of time. We also know that the ampere’s circuital law is the line integral of the magnetic field is equal to the sum of the current in the closed loop.
$\mu_{0}I=\oint{\vec{B}.d\vec{l}}$
In ACD, the area vector is the perpendicular to the surface and acts towards the upward direction, while in ABC, it acts along the right direction.
From the figure, we can see that in loop ABC, the $I_{1}$ and $I_{3}$ are in the opposite direction, similarly, in loop ADC, the $I_{2}$ and $I_{3}$ are in the opposite direction, then we can say the total current enclosed in the loop is given as $I=I_{1}+I_{2}+I_{3}-I_{3}$
$\implies I=I_{1}+I_{2}$
Then we have
$\mu_{0}(I_{1}+I_{2})=\oint{\vec{B}.d\vec{l}}$
Additional information:
From Biot-Savart law we know that the magnetic field B produced at a point near a current carrying conductor is proportional to the material of the medium$\mu_{0}$, the current $I$ flowing in the conductor, the small length of the wire $dl$involved and inversely proportional to distance $r$between the point and the conductor.
Mathematically, $dB \propto \mu_{0}$ , $dB\propto I$, $dB \propto dl$ and $dB \propto\dfrac{1}{r^{2}}$
Then,$dB= \dfrac{\mu_{0}}{4\pi}\times \dfrac{Idlsin\theta}{r^{2}}$, where $\theta$ is the angle between $dl$ and $r$ .

Note:
Ampere’s circuital law can be expressed in two ways, one in the integral and the other in the form of differentiation. Here, since it is mentioned in the question to use integral form we are doing so. However, it is important to note that this is one law which gives the relation between current and magnetism.