Question

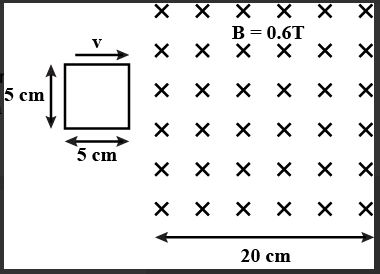
Figure shows a square loop of side $ 5\;cm\; $ being moved towards right at a constant speed of $ 1cmse{c^{ - 1}} $ . The front edge just enters the $ 20\;cm\; $ wide magnetic field at $ t = 0 $ . Find the induced emf in the loop at $ t = 2s\; $ and $ t = 10s $ .

 $ \left( A \right)3 \times {10^{ - 2}},zero \\
  \left( B \right)3 \times {10^{ - 2}},3 \times {10^{ - 4}} \\
  \left( C \right)3 \times {10^{ - 4}},3 \times {10^{ - 4}} \\
  \left( D \right)3 \times {10^{ - 4}},zero \\ $

Answer 1

Hint :In order to solve this question, we are going to first find the distance travelled by the coil inside the magnetic field in the time interval $ t = 2s $ , then, the change in flux can be calculated which gives us the induced emf for this interval, now for $ t = 10s $ , coil is completely inside the field, so emf value is accordingly.
The formula for distance covered by the coil moving with velocity $ v $ in time $ t $
 $ d = vt $
Flux for magnetic field $ B $ through area $ A $ is
 $ \phi = BA $

Complete Step By Step Answer:
As it is given in the question, that the initial speed of the loop is
 $ u = 1cm{s^{ - 1}} $
Magnetic field, $ B = 0.6T $
At $ t = 2s $ ,
Distance moved by the coil is
  $ d = vt \\
   \Rightarrow d = 2cm = 2 \times {10^{ - 2}}m \\ $
Now, the area under the magnetic field at $ t = 2s $
 $ A = 2 \times 5 \times {10^{ - 4}}{m^2} \\
   \Rightarrow A = {10^{ - 3}}{m^2} \\ $
Now the initial flux inside the loop is zero because the loop is outside the magnetic field
And the final flux can be calculated as
 $ \phi = BA = 0.6 \times {10^{ - 3}} $
Therefore, the change in flux becomes
 $ \Delta \phi = 0.6 \times {10^{ - 3}} $
Therefore, the induced emf for the square loop is
 $ e = \dfrac{{\Delta \phi }}{{\Delta t}} = \dfrac{{0.6 \times {{10}^{ - 3}}}}{2} = 0.3 \times {10^{ - 3}}V \\
   \Rightarrow e = 3 \times {10^{ - 4}}V \\ $
We are given the velocity is $ 1cmse{c^{ - 1}} $ , and the distance inside the field that the loop is travelling is $ 20cm $ , therefore, the time period is $ 20\sec $
Therefore, at time $ t = 10s $ , the coil is completely inside the magnetic field, hence there is no change in the magnetic flux at that time, so the induced emf is equal to zero.
Hence, option $ \left( D \right)3 \times {10^{ - 4}},zero $ is correct.

Note :
The induced emf depends upon the change in the flux in the loop which can be caused due to any of the reasons like entering or leaving a magnetic field, change in the value of magnetic field due to change in current, but when a coil moves just inside the field with no change in the field, the flux is zero.