Question

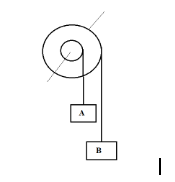
Figure shows a small wheel fixed coaxially on a bigger one of the double of the radius. The system rotates about the common axis. The strings supporting A and B do not slip on the wheels. If $x$and $y$be the distance travelled by A and B in the same time interval, then

A.)$x=2y$
B.)$x=y$
C.)$y=2x$
D.)$\text{none of these}$

Answer 1

Hint: Angular velocity of both the wheels would be the same and hence their angular momentum. By applying the equation of motion and angular momentum we will solve the numerical.

Formulae used:

$\begin{align}
  & v=r\omega \\
 & \text{distance = speed}\times \text{time} \\
\end{align}$

Complete step by step answer:
The distances travelled by A and B are given as $x$and $y$respectively. As the two masses do not slip, it means that they are moving with the same angular velocity.
Angular velocity is defined as the rate of velocity at which an object or a particle is rotating around a center in a given period of time. It is measured in angle per unit time or we can say radians per second.

Take the radius of pulley associated with mass A as \[R\] and that of B as$2R$.

Angular velocity of mass A,${{v}_{A}}=\omega R$
Angular velocity of mass B,${{v}_{B}}=\omega \times 2R$
Distance travelled by A = $x={{v}_{A}}t=\omega Rt$
Distance travelled by B =$y={{v}_{B}}t=\omega \times 2R\times t$

Substituting value of $\omega Rt$ from equation $x={{v}_{A}}t=\omega Rt$ to equation $y={{v}_{B}}t=\omega \times 2R\times t$

We get, $y=\omega \times 2R\times t=2\omega Rt=2x$

$y=2x$

Linear distance covered by mass B is double of the distance covered by mass A.
Hence, the correct option is C.

Note:
Students should not get confused between linear velocity and angular velocity of an object. Linear velocity is the rate of change in position of a body in a given time, while angular velocity means how much a body spins or rotates around a fixed point. In the above question, angular velocities of both masses A and B were the same but linear distance travelled by them was different and hence their linear velocities were also different.