Question

Figure shows a rod of length $20\;cm$ pivoted at one end and is made to rotate in a horizontal plane with a constant angular speed. A ball of mass$\;m$ is suspended by a string also of length$\;20\;cm$ from the other end of the rod. If the angle $\theta$ made by the string with the vertical is$\;30$, find the angular speed of the rotation. Take $g=10\;ms^{-2}$.

A). $\omega = 8\;rads^{-1}$
B). $\omega = 4.4\;rads^{-1}$
C). $\omega = 14.4\;rads^{-1}$
D). $\omega = 44.4\;rads^{-1}$

Answer 1

Hint: The motion of the ball by virtue of the rotation of the rod traces a circular path about the pivot as its centre. In such a case, first determine the radius of the path traced. Use this to determine the outwardly directed centrifugal force experienced by the ball. Then use free-body diagrams to equate horizontal and vertical components of the individual forces and evaluate them to arrive at an expression for the angular speed of rotation. To this end, plug in the given values into the expression to arrive at an appropriate solution.
Formula Used:
Centrifugal force $F_c = m\omega^2 r$

Complete step-by-step solution:
We are given that a ball of mass$\;m$ is suspended by a string of length $L=20\;cm$ attached to the end of a rod of length $L=20\;cm$. The rod is made to rotate about its pivot, which makes the ball also rotate with the rod, keeping the string at an angle $\theta=30^{\circ}$ with the vertical. We look at the forces under which the ball-string system is subjected to as shown in the figure.

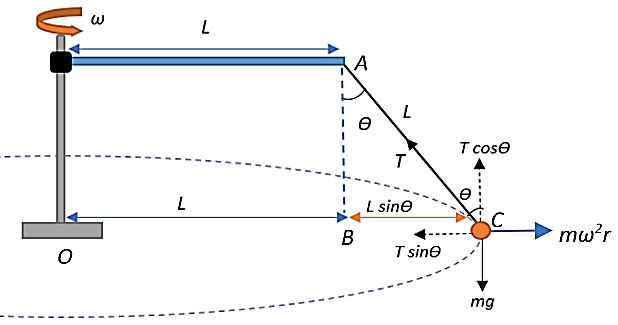
We see that as a result of the rod’s motion and the ball’s suspension, the string experiences a tension$\;T$. This tension can be resolved into its horizontal and vertical components. Further, the massiveness of the ball imparts a gravitational force or weight to the ball that is directed vertically downward as shown. Additionally, the ball is also subject to a centrifugal force directed outwards as a result of it being swung about the string as the rod rotates with an angular speed of $\omega$.
The path that the ball traces as it rotates with the rod is shown, and we see that it moves in a circle with the pivot as the centre. From the figure, the radius of the circle traced by the path will be:
$r = OB + BC = L+BC$
From $\Delta ABC$, we have:
$sin\theta = \dfrac{BC}{AC} \Rightarrow BC = AC \;sin\theta = Lsin\theta$
Therefore, $r = L+ BC = L+L\;sin\theta = L(1+sin\theta)$
This means that the centrifugal force acting on the ball will be:
$F_{c} = m\omega^2 r = m\omega^2L(1+sin\theta)$
Now, from the diagram, we see that:
$T\;cos\theta = mg$
$T\;sin\theta = F_c = m\omega^2L(1+sin\theta)$
Dividing the above two equations we get:
$\dfrac{T\;sin\theta}{T\;cos\theta} = \dfrac{m\omega^2L(1+sin\theta)}{mg}$
$\Rightarrow tan\theta = \dfrac{\omega^2L(1+sin\theta)}{g}$
Rearranging the above equation to get an expression for angular speed:
$\Rightarrow \omega = \sqrt{\dfrac{tan\theta \times g}{L(1+sin\theta)}}$
Taking $\theta = 30^{\circ}, \;L= 20\;cm = 0.2\;m$ and $g = 10\;ms^{-1}$, we get:
$\omega = \sqrt{\dfrac{\left(\dfrac{1}{\sqrt{3}}\right) \times 10}{0.2 \times \left(1 + \dfrac{1}{2}\right)}} = \sqrt{\dfrac{0.577 \times 10}{0.2 \times 1.5}} = \sqrt{\dfrac{5.77}{0.3}} = \sqrt{19.23}$
$\Rightarrow \omega = 4.39 \approx 4.4\;rads^{-1} $
Therefore, the correct choice would be B. $\omega = 4.4\;rads^{-1}$

Note: It is important to understand the distinction between linear velocity (v) and angular velocity ($\omega$) and establish a relationship between the two. Linear velocity is generally associated with linear displacements or linear motion which is any motion that occurs along a straight line in one direction, whereas angular velocity is associated with angular displacements or rotatory motion which is any motion where a body moves in a circular path about an axis of rotation.
Linear velocity $v = r\omega$
Note that though linear velocity is associated with straight line motion, it is also a measurable quantity in circular motion in addition to the angular velocity. The linear velocity at a point is directed tangentially away from the radius of the path, whereas the angular velocity is directed radially.