Question

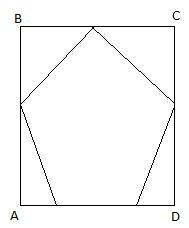
Figure shows a regular pentagon with all of its vertices on the sides of a rectangle. If $BC=\dfrac{1}{4}$, calculate the perimeter of the pentagon.

(a) 0.31
(b) 0.62
(c) 0.77
(d) 0.80
(e) 1.00

Answer 1

Hint: Use the sine rule given by: $\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$, where a, b and c are the length of sides of the triangle and A, B and C are the angles opposite to that of sides a, b and c respectively. Assume the length of one of the sides of pentagon as $x$. Determine the value of $x$ using the sine rule and multiply this value with 5 to get the perimeter.

Complete step-by-step answer:
We know that all the sides of a regular pentagon are equal. Let us assume each side is $x$. Let us name the pentagon, MNOPQ as shown in the figure.
Let us join the vertices N and Q to form a triangle MNQ. Also, there is a rectangle BNQC formed.

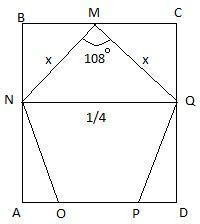
NQ = BC = $\dfrac{1}{4}$, since they are the opposite sides of the rectangle BNQC.
Now, in triangle MNQ,
Angle NMQ = ${{108}^{\circ }}$, since all the internal angles of a regular pentagon is ${{108}^{\circ }}$.
Also, MN = MQ, since all the sides of a regular pentagon are equal.
Therefore, $\angle MNQ=\angle MQN={{36}^{\circ }}$.
Now, applying sine rule in triangle MNQ, we get,
$\dfrac{MN}{\sin {{36}^{\circ }}}=\dfrac{NQ}{\sin {{108}^{\circ }}}$
Using, NQ = BC = $\dfrac{1}{4}$, we get,
$\begin{align}
  & \dfrac{MN}{\sin {{36}^{\circ }}}=\dfrac{NQ}{\sin {{108}^{\circ }}} \\
 & \Rightarrow \dfrac{x}{\sin {{36}^{\circ }}}=\dfrac{1}{4\sin {{108}^{\circ }}} \\
\end{align}$
Now using, the conversion: $\sin {{108}^{\circ }}=\sin \left( {{180}^{\circ }}-{{108}^{\circ }} \right)=\sin {{72}^{\circ }}$ and the identity, $\sin 2x=2\sin x\cos x$, we get,
$\begin{align}
  & x=\dfrac{\sin {{36}^{\circ }}}{4\times 2\sin {{36}^{\circ }}\cos {{36}^{\circ }}} \\
 & \Rightarrow x=\dfrac{1}{8\cos {{36}^{\circ }}} \\
\end{align}$
Substituting, $\cos {{36}^{\circ }}=\dfrac{\sqrt{5}+1}{4}$, we get,
$\begin{align}
  & x=\dfrac{1}{8\times \dfrac{\sqrt{5}+1}{4}} \\
 & \Rightarrow x=\dfrac{1}{2}\times \dfrac{1}{\sqrt{5}+1} \\
\end{align}$
Rationalizing the denominator we get,
$\begin{align}
  & x=\dfrac{1}{2}\times \dfrac{1}{\sqrt{5}+1}\times \dfrac{\sqrt{5}-1}{\sqrt{5}-1} \\
 & =\dfrac{1}{2}\times \dfrac{\sqrt{5}-1}{5-1} \\
 & =\dfrac{\sqrt{5}-1}{8} \\
\end{align}$
Substituting, $\sqrt{5}=2.236$, we have,
$\begin{align}
  & x=\dfrac{2.236-1}{8} \\
 & \Rightarrow x=\dfrac{1.236}{8} \\
 & \Rightarrow x=0.1545 \\
\end{align}$
Now, the perimeter of the pentagon $=5x$, because all the 5 sides are equal.
$\Rightarrow perimeter=5\times 0.1545\approx 0.77$
Hence, option (c) is the correct answer.

Note: One may note that we have joined the vertices NQ of the pentagon. The reason is that, we only know the length of the side BC of the rectangle. We can also apply cosine rule instead of sine rule in the triangle MNQ, but that will only elongate the expression. Therefore, we have applied sine rule to make the expression simple.