Question

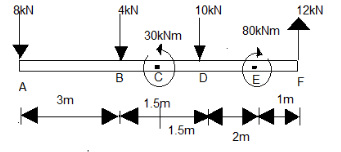
Figure shows a parallel system of four forces and two couples.
(i) Replace it by a single force and obtain its location from point $ A $
(ii) Replace it by a force couple system at point $ A $
(iii) Replace it by a force couple system at point $ D $
(iv) Replace it by two parallel forces at $ B $ and $ D $

Answer 1

Hint: In order to solve this question, we are going to calculate the torque at point $ A $, then considering a variable for the distance and dividing by force and equating to the torque, distance is calculated. Similarly, other parts are solved for the other values of forces and torques as well.
Formula used: Torque at any point is given by
  $ \Rightarrow {\tau _A} = {F_A} \times x $

Complete step by step solution:
Let us consider the point $ A $ , the torque at the point $ A $ is due to the forces $ 4kN $ , $ 10kN $ and $ 12kN $ , also due to the two couple forces $ 30kNm $ and $ 80kNm $ , thus, if we find the torque about the point $ A $ , then,
$ {\tau _A} = 4kN \times 3 + 10kN \times 6 - 30kNm + 80kNm - 12kN \times 9 \\
   \Rightarrow {\tau _A} = 12 + 60 - 30 + 30 - 108 \\
   \Rightarrow {\tau _A} = 152 - 138 \\
   \Rightarrow {\tau _A} = 14kNm $
Now as we know that the net torque can be related to the net force as
 $ \Rightarrow {\tau _A} = {F_A} \times x $
Putting values of net force at $ A $ and the net torque at $ A $ to find the distance
$ \Rightarrow 14kNm = 10kN \times x \\
   \Rightarrow x = 1.4m $
Now if we find the net force at the point $ A $ in $ y - direction $
$ {F_{net}} = - 8 - 4 - 10 + 12 \\
   \Rightarrow {F_{net}} = - 10kN $
The net torque about $ A $ is
$ {\tau _{net}} = 4kN \times 3m + 10kN \times 6m - 30kNm + 80kNm - 12kN \\
   \Rightarrow {\tau _{net}} = 12 + 60 - 30 + 80 - 108 \\
   \Rightarrow {\tau _{net}} = 152 - 138 \\
   \Rightarrow {\tau _{net}} = 14kNm $
Now at point $ D $ ,
The net torque is
 $ {\tau _D} = 8kN \times 4.5m + 4kN \times 1.5m - 30kNm + 10kN \times 1.5m + 80kNm - 12kN \times 3m \\
  \Rightarrow {\tau _D} = 3.6 + 6 - 30 + 15 + 80 - 36 \\
   \Rightarrow {\tau _D} = 38.6kNm $
At point $ B $ and $ D $
The net force is
$ {F_B} = - 8 - 4 - 10 + 12 - \dfrac{{30}}{{1.5}} + \dfrac{{80}}{5} \\
   \Rightarrow {F_B} = - 14kN $
These two parallel forces are of magnitude $ 14kN $ each but in opposite directions.

Note:
The forces to replace the two couple forces are calculated step by step at all the points, when we needed to find the couple forces the torques were calculated while in the other parts, where directly the forces were asked, the force was calculated at that point.