Question

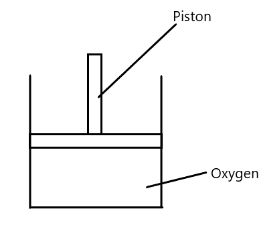
Figure below shows a cylindrical container containing oxygen and closed by a 50 kg frictionless piston. The area of the cross section is $ 100c{m^2} $ , atmospheric pressure is 100kPa and $ g $ is $ 10m/{s^2} $ . The cylinder is slowly heated for some time. Find the amount of heat supplied to the gas if the piston moves out through a distance of 20 cm.Ω

Answer 1

Hint : Since, the piston is free to move out, there is no change in internal energy. The work done is equal to the pressure multiplied by the change in volume.

Formula used: In this solution we will be using the following formula;
 $\Rightarrow W = \Delta Q $ where $ W $ is the work done by the system and $ \Delta Q $ is the heat supplied to the system. $ W = P\Delta V $ where $ P $ is the pressure of the gas, $ \Delta V $ is the change in volume of the system.
 $\Rightarrow P = \dfrac{F}{A} $ , where $ F $ is the force exerted on an area $ A $ .
 $\Rightarrow W = mg $ is the weight of an object, $ m $ is the mass and $ g $ is the acceleration due to gravity.

Complete step by step answer
According to the question, a piston rests on a cylindrical container containing oxygen. The weight of this piston hence is exerted on the gas. And since it is in equilibrium (no acceleration), the total force exerted by the piston (due to the weight of the piston and the atmospheric pressure) must be balanced by an equal and opposite force exerted by the gas on the piston due to the pressure build up in the gas. Hence
 $\Rightarrow F = W + {P_{atm}}A = PA $ where $ F $ is the force exerted by the piston, $ W $ is weight of the piston, $ {P_{atm}} $ is the atmospheric pressure, $ P $ is the pressure of the gas and $ A $ is the cross section area.
Can be written as
 $\Rightarrow PA = mg + {P_{atm}}A $
Hence, by insertion of all known values and conversion to SI unit, we have,
 $\Rightarrow P(100 \times {10^{ - 4}}) = (50 \times 10) + 100 \times {10^3}\left( {100 \times {{10}^{ - 4}}} \right) $ (since $ 1{m^2} = {10^{ - 4}}c{m^2} $ and $ 1kPa = {10^3}Pa $ )
By computing we have
 $\Rightarrow 0.01P = 500 + 1000 = 1500 $
Hence we get,
 $\Rightarrow P = \dfrac{{1500}}{{0.01}} = 150000Pa $
Now, after the heat is applied, the piston moves out through a distance of 20 cm. Hence, the work done by the gas on the piston is given by
 $\Rightarrow W = P\Delta V = PA\Delta h $ where $ \Delta V $ is the increase in volume, and $ \Delta h $ is the increase in height.
Thus,
 $\Rightarrow W = 150000 \times 100 \times {10^{ - 4}} \times 20 \times {10^{ - 2}} = 300{\text{J}} $
Since the piston was allowed to move freely, it is given that
 $\Rightarrow W = \Delta Q $ hence, the heat applied $ \Delta Q $ is
 $\therefore \Delta Q = 300{\text{J}} $ .

Note
In general, the equation governing such thermodynamic situation is the first law of thermodynamics given mathematically as,
 $\Rightarrow \Delta U = \Delta Q - W $ where $ \Delta U $ is the change in internal energy of the system, $ \Delta Q $ is the heat applied to the system and $ W $ is the work done by the system. It is understood that thermodynamic systems seek to maintain its potential energy, hence, for a frictionless piston, when the heat is applied, the system is allowed to do work without resistance. Thus, all the internal energy is converted to work.
Hence, $ \Delta U $ is zero and
 $\Rightarrow W = \Delta Q $ .