Question

Fig. shows a brick of weight \[\text{2kgf}\] and dimensions \[20\text{cm }\times \text{ 10cm }\times \text{ 5cm}\] placed in three different positions on the ground. Find the pressure exerted by the brick in each case.

Answer 1

Hint: For each case, the force acting on the brick is its weight. The area in contact with the ground is the effective area. Substitute the values of force and effective area in the formula for pressure to calculate in each case. Convert the units accordingly.
Formulas Used: \[\text{w = mg}\]
\[\text{Pressure ( }\!\!\rho\!\!\text{ ) = }\dfrac{\text{Force (f)}}{\text{Effective Area (a)}}\]

Complete answer:
Weight is defined as the force exerted by the earth on a body near its surface due to gravity. Weight is given by the formula-
\[\text{w = mg}\] - (1)
Where, m is the mass of the body
g is acceleration due to gravity, \[\text{g = 10m}{{\text{s}}^{-2}}\]
\[\text{kgf}\]is a unit of gravitational force such that \[\text{1 kgf}\] is equal to 10 N, so,
\[\text{2 kgf= 2}\times \text{ 10 N= 20 N}\] - (2)
Force applied on or by a body per unit area is called pressure. The direction of pressure is always perpendicular to the surface of the body. It’s SI unit is Pa.
\[\text{Pressure ( }\!\!\rho\!\!\text{ ) = }\dfrac{\text{Force (f)}}{\text{Effective Area (a)}}\] - (3)
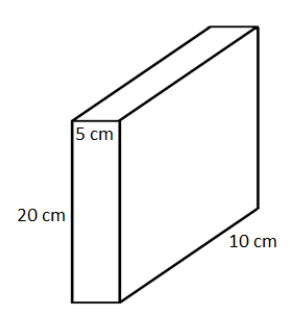
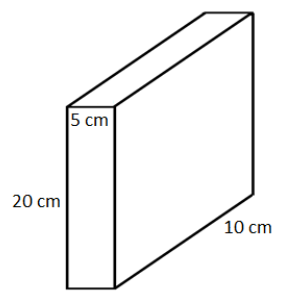
In fig. 1,

\[\text{a = 10 }\times \text{ 1}{{\text{0}}^{-2}}\text{m }\times \text{ 20 }\times \text{ 1}{{\text{0}}^{-2}}\text{m}\]
From eq (2) and eq (3), we get,
\[\text{ }\!\!\rho\!\!\text{ = }\dfrac{20}{10\text{ }\times \text{ 1}{{\text{0}}^{-2}}\text{ }\times \text{ 20 }\times \text{ }{{10}^{-2}}}\text{ Pa}\]
\[\text{ }\!\!\rho\!\!\text{ = 1000 Pa}\]
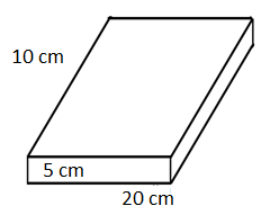
In fig. 2,

\[\text{a = 5 }\times \text{ 1}{{\text{0}}^{-2}}\text{m }\times \text{ 10 }\times \text{ }{{10}^{-2}}\text{m}\]
From eq (2) and eq (3), we get,
\[\text{ }\!\!\rho\!\!\text{ =}\dfrac{20}{5\text{ }\times \text{ }{{10}^{-2}}\text{ }\times \text{ 10 }\times \text{ 1}{{\text{0}}^{-2}}}\text{ pa}\]
\[\text{ }\!\!\rho\!\!\text{ = 4000 Pa}\]
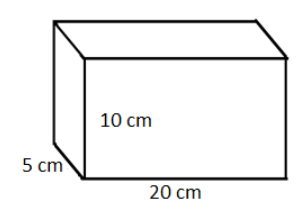
In fig. 3,

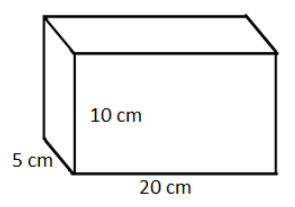
\[\text{a = 5 }\times \text{ 1}{{\text{0}}^{-2}}\text{m }\times \text{ 20 }\times \text{ 1}{{\text{0}}^{-2}}\text{m}\]
from eq (2) and eq (3) , we get,
\[\text{ }\!\!\rho\!\!\text{ = }\dfrac{20}{5\text{ }\times \text{ 1}{{\text{0}}^{-2}}\text{ }\times \text{ 20 }\times \text{ }{{10}^{-2}}}\text{ Pa}\]
\[\text{ }\!\!\rho\!\!\text{ = 2000 Pa}\]
Therefore, the pressure in fig. 1 is, \[\text{ }\!\!\rho\!\!\text{ = 1000 Pa}\]
Pressure in fig. 2 is, \[\text{ }\!\!\rho\!\!\text{ = 4000 Pa}\]
Pressure in fig. 3 is, \[\text{ }\!\!\rho\!\!\text{ = 2000 Pa}\]

Additional Information:
The SI unit of weight is\[\text{N}\]. The other units of force includes; kgf, dyne, gram-force, poundal, pound-force etc

Note:
\[\text{Pa = N}{{\text{m}}^{-2}}\] therefore units of force and area need to be converted to \[\text{N}\] and \[{{\text{m}}^{\text{2}}}\] otherwise the answer will be wrong. Effective area is the area which is in contact with the ground and on which the pressure is being applied to. As effective area increases pressure decreases and vice versa.