Question

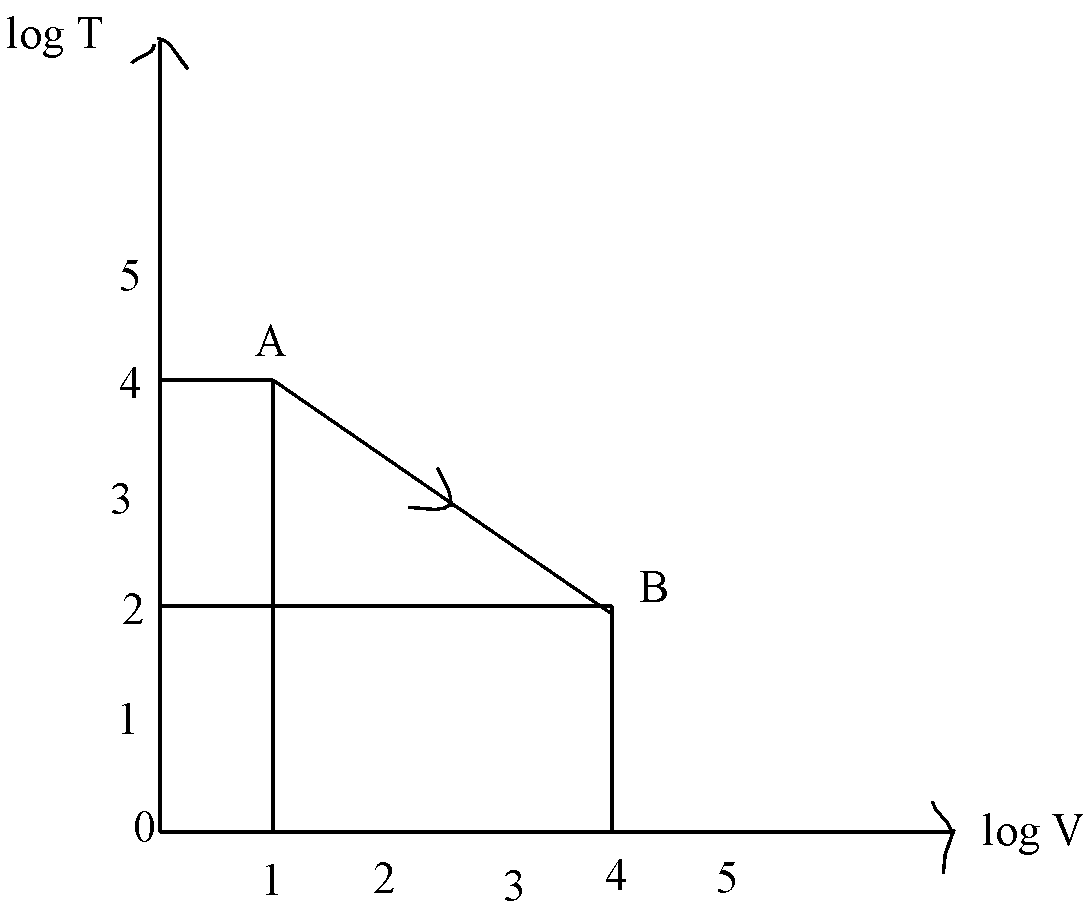
Fig shown, the adiabatic curve on a log T and log V scale performed on ideal gas. The gas is:

(a) Monoatomic
(b) Diatomic
(c) Polyatomic
(d) Mixture of monoatomic and diatomic

Answer 1

Hint: Adiabatic process in which there is no transfer of heat. When we plot the adiabatic process between V and T, the equation is $T{{V}^{\gamma -1}}=K$, K is the constant. This equation is converted into a log form and compared with the straight-line equation and the slope is calculated. With the slope we can find the value of $\gamma $ and tell the nature of the gas.

Complete step by step answer:
An adiabatic is a process in which there is no change in the heat, but the value of pressure, volume, and temperature changes or we can say that the system is separated from the adiabatic wall.
In the figure, the graph is between log V and log T.
So, the adiabatic equation in the volume and temperature form is:
$T{{V}^{\gamma -1}}=K$
Where $\gamma $is the ratio ${{C}_{p}}/{{C}_{v}}$ and K is the constant.
On converting this equation in log form we get:
$\log T+(\gamma -1)\log V=\log K$
This equation can be compared with the straight line equation:
$y+mx=c$
m is the slope and it is equal to $(\gamma -1)$
From the figure the slope can be calculated as:
$m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
$m=\dfrac{4-2}{4-1}=\dfrac{2}{3}$
So, we can write:
$\gamma -1=\dfrac{2}{3}$
From this we get $\gamma $:
$\gamma =\dfrac{5}{3}$
This value is for monoatomic gas.
Therefore, the correct answer is an option (a)- Monoatomic.

Note: The value of $\gamma $for monatomic gas is $\dfrac{5}{3}$ , for diatomic gas is $\dfrac{7}{5}$, and for polyatomic gas is $\dfrac{9}{7}$. If the relation is calculated between P and V, the formula is $P{{V}^{\gamma }}=K$ and if the relation is between P and T, the formula is ${{P}^{\gamma -1}}{{T}^{\gamma }}=K$.