Question

FCS \[y={{\exp }_{fcs}}(x;1)={{e}^{x+{{e}^{x+{{e}^{x+......}}}}}}\]. How do you prove that, as \[y\to \infty ,y+x\to C<\infty \]?

Answer 1

Hint: For answering this question we need to prove that when $y\to \infty $ then the value of $y+x\to C<\infty $ where the value of $y$ is given \[y={{\exp }_{fcs}}(x;1)={{e}^{x+{{e}^{x+{{e}^{x+......}}}}}}\] . We know that we can write this expression simply as $y={{e}^{x+y}}$ . Now we will apply logarithm on both sides and differentiate it with respect to $x$ and derive the turning point.

Complete step by step solution:From the question, we were given \[y={{\exp }_{fcs}}(x;1)={{e}^{x+{{e}^{x+{{e}^{x+......}}}}}}\].
Let us assume
\[y={{\exp }_{fcs}}(x;1)={{e}^{x+{{e}^{x+{{e}^{x+......}}}}}}.....(1)\]
Now let us substitute equation (1) in equation (1). Then we get
\[\Rightarrow y={{e}^{x+y}}\]
Now let us apply logarithms on both sides. Then we get
\[\Rightarrow \ln y=\ln {{e}^{x+y}}\]
From the basics concepts, we already know that \[\ln {{e}^{f(x)}}=f(x)\].
So, we get
\[\begin{align}
  & \Rightarrow \ln y=x+y \\
 & \Rightarrow \ln y-y=x \\
\end{align}\]
Now let us consider
\[\Rightarrow \ln y-y=x...(2)\]
Now by differentiating equation (2) on both sides with respect to $x$ , then we get
\[\begin{align}
  & \Rightarrow \dfrac{d}{dx}(\ln y-y)=\dfrac{dx}{dx} \\
 & \Rightarrow \dfrac{d}{dx}\ln y-\dfrac{dy}{dx}=1 \\
\end{align}\]
We already know that \[\dfrac{d}{dx}\ln x=\dfrac{1}{x}\]. So by using this we will have
\[\begin{align}
  & \Rightarrow \dfrac{1}{y}\dfrac{dy}{dx}-\dfrac{dy}{dx}=1 \\
 & \Rightarrow \dfrac{dy}{dx}\left( \dfrac{1}{y}-1 \right)=1 \\
 & \Rightarrow \dfrac{dy}{dx}\left( \dfrac{1-y}{y} \right)=1 \\
 & \Rightarrow \dfrac{dy}{dx}=\dfrac{y}{1-y} \\
\end{align}\]
Now let us rearrange this equation as shown below:
\[\begin{align}
  & \Rightarrow \dfrac{dx}{dy}=\dfrac{1-y}{y} \\
 & \Rightarrow \dfrac{dx}{dy}=\dfrac{1}{y}-1 \\
\end{align}\]
If \[\dfrac{dx}{dy}\] is equal to 0, then we get
\[\begin{align}
  & \Rightarrow 0=\dfrac{1}{y}-1 \\
 & \Rightarrow \dfrac{1}{y}=1 \\
 & \Rightarrow y=1 \\
\end{align}\]
If \[y\to \infty \], then we get
\[\Rightarrow \dfrac{dx}{dy}=-1\]
So, we can say that \[\left( -1,1 \right)\] is the turning point.

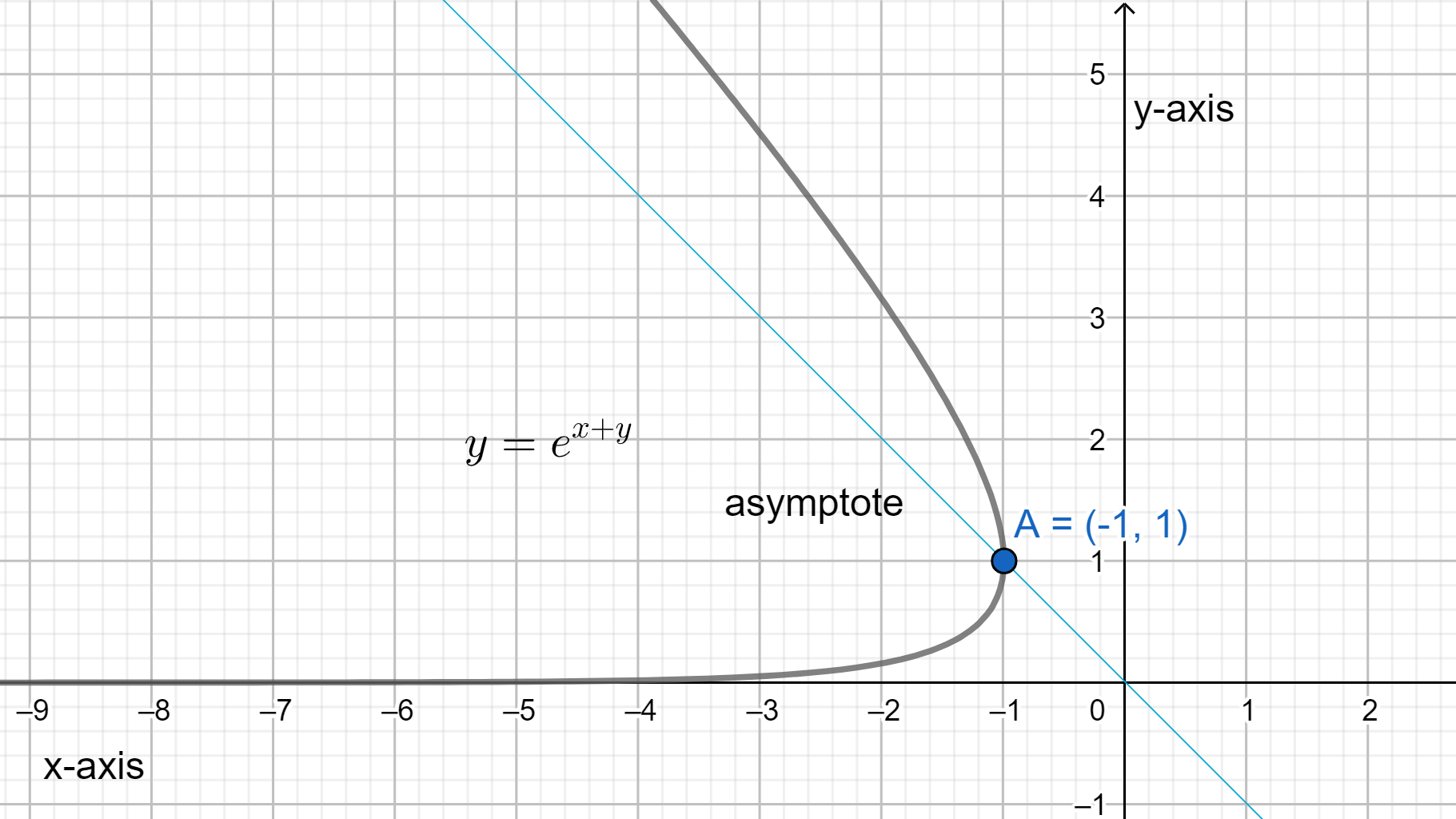
By seeing this plot, we can say that the asymptote \[x+y=0\] cuts the FCS near O. So, the graph turns towards this direction of \[x+y=0\] to align with all such linear and non-linear curves. So, all the parallel lines \[x+y=C\] also in the direction polar \[\theta =\dfrac{3\pi }{4}\].


Note: This is a very confusing and tricky question we should handle the steps we perform during the solution very carefully. The definition of an asymptote is given as “a line or curve that approaches a given curve arbitrarily closely”.