
Factorize the given polynomial \[{x^3} - 7x + 6\]
Answer
569.4k+ views
Hint: For this model first find out the one factor of the given polynomial by using trial method .Then after getting the one factor use the division method by using that factor . Use the formula \[dividend = divisor \times quotient + remainder\] for further simplification.
Complete step-by-step answer:
Given polynomial , \[{x^3} - 7x + 6\]
Let us take the given polynomial as \[p\left( x \right) = {x^3} - 7x + 6\]
Let us consider all the factors of the \[6\].
By using trial method
Let us substitute \[ - 1\] in the place of x. we get
\[\
p\left( { - 1} \right) = {\left( { - 1} \right)^3} - 7\left( { - 1} \right) + 6 \\
\,\,\,\,\,\,\,\,\,\, = - 1 - 7 + 6 \\
\,\,\,\,\,\,\,\,\,\, = - 2 \ne 0 \\
\ \]
Therefore, \[\left( {x + 1} \right)\] is not the factor of a given polynomial.
Again let us substitute \[1\] in the place of x . we get,
\[\
p\left( 1 \right) = {\left( 1 \right)^3}^{} - 7\left( 1 \right) + 6 \\
\,\,\,\,\,\,\,\,\,\, = 1 - 7 + 6 \\
\,\,\,\,\,\,\,\,\,\, = 0 \\
\ \]
Therefore , \[\left( {x - 1} \right)\] is a factor of the given polynomial.
Now , let us find the quotient on dividing \[{x^3} - 7x + 6\] by \[\left( {x - 1} \right)\]
This can be solved by using method of long division
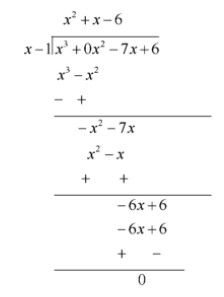
We know that ,
\[dividend = divisor \times quotient + remainder\]
Therefore , \[\
{x^3} - 7x + 6 = \left( {x - 1} \right) \times \left( {{x^2} + x - 6} \right) + \left( 0 \right) \\
{x^3} - 7x + 6 = \left( {x - 1} \right) \times \left( {{x^2} + x - 6} \right).....\left( 1 \right) \\
\ \]
Let us consider \[q\left( x \right) = {x^2} + x - 6\]
Let us find the factors of the \[q\left( x \right) = {x^2} + x - 6\] by using factorization method
Comparing \[q\left( x \right) = {x^2} + x - 6\] with expression with \[a{x^2} + bx + c\]. We get \[a = 1,b = 1,c = - 6\]
Now multiply “a” term with “c” term and factor the product of (ac) such that the sum of factors equals to b .
The product of a, c is \[1\left( { - 6} \right) = - 6\]. Factor -6 as -2,3such that the sum of factors (-2)+3=1 which equals a coefficient of x that is b.
That is \[{x^2} + x - 6 = {x^2} + 3x - 2x - 6\]
In the next step , we are taking x as common in first two terms and -2 as common in next two terms
\[ = x\left( {x + 3} \right) - 2\left( {x + 3} \right)\]
Now taking \[\left( {x + 3} \right)\] from above equation
\[ = \left( {x + 3} \right)\left( {x - 2} \right)\]
Now substitute above factors in equation (1) , we get
\[\
{x^3} - 7x + 6 = \left( {x - 1} \right) \times \left[ {\left( {x + 3} \right) \times \left( {x - 2} \right)} \right] \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {x - 1} \right)\left( {x + 3} \right)\left( {x - 2} \right) \\
\ \]
Thus , the factors of the given polynomial are \[\left( {x - 1} \right)\left( {x + 3} \right)\left( {x - 2} \right)\]
Note: Factorization method is the process of factoring a polynomial into factors for which we use the several methods they are trial and error method, division method and the remainder theorem.
Complete step-by-step answer:
Given polynomial , \[{x^3} - 7x + 6\]
Let us take the given polynomial as \[p\left( x \right) = {x^3} - 7x + 6\]
Let us consider all the factors of the \[6\].
By using trial method
Let us substitute \[ - 1\] in the place of x. we get
\[\
p\left( { - 1} \right) = {\left( { - 1} \right)^3} - 7\left( { - 1} \right) + 6 \\
\,\,\,\,\,\,\,\,\,\, = - 1 - 7 + 6 \\
\,\,\,\,\,\,\,\,\,\, = - 2 \ne 0 \\
\ \]
Therefore, \[\left( {x + 1} \right)\] is not the factor of a given polynomial.
Again let us substitute \[1\] in the place of x . we get,
\[\
p\left( 1 \right) = {\left( 1 \right)^3}^{} - 7\left( 1 \right) + 6 \\
\,\,\,\,\,\,\,\,\,\, = 1 - 7 + 6 \\
\,\,\,\,\,\,\,\,\,\, = 0 \\
\ \]
Therefore , \[\left( {x - 1} \right)\] is a factor of the given polynomial.
Now , let us find the quotient on dividing \[{x^3} - 7x + 6\] by \[\left( {x - 1} \right)\]
This can be solved by using method of long division
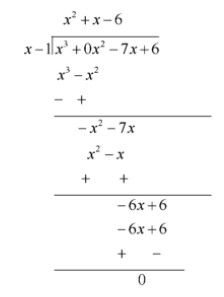
We know that ,
\[dividend = divisor \times quotient + remainder\]
Therefore , \[\
{x^3} - 7x + 6 = \left( {x - 1} \right) \times \left( {{x^2} + x - 6} \right) + \left( 0 \right) \\
{x^3} - 7x + 6 = \left( {x - 1} \right) \times \left( {{x^2} + x - 6} \right).....\left( 1 \right) \\
\ \]
Let us consider \[q\left( x \right) = {x^2} + x - 6\]
Let us find the factors of the \[q\left( x \right) = {x^2} + x - 6\] by using factorization method
Comparing \[q\left( x \right) = {x^2} + x - 6\] with expression with \[a{x^2} + bx + c\]. We get \[a = 1,b = 1,c = - 6\]
Now multiply “a” term with “c” term and factor the product of (ac) such that the sum of factors equals to b .
The product of a, c is \[1\left( { - 6} \right) = - 6\]. Factor -6 as -2,3such that the sum of factors (-2)+3=1 which equals a coefficient of x that is b.
That is \[{x^2} + x - 6 = {x^2} + 3x - 2x - 6\]
In the next step , we are taking x as common in first two terms and -2 as common in next two terms
\[ = x\left( {x + 3} \right) - 2\left( {x + 3} \right)\]
Now taking \[\left( {x + 3} \right)\] from above equation
\[ = \left( {x + 3} \right)\left( {x - 2} \right)\]
Now substitute above factors in equation (1) , we get
\[\
{x^3} - 7x + 6 = \left( {x - 1} \right) \times \left[ {\left( {x + 3} \right) \times \left( {x - 2} \right)} \right] \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {x - 1} \right)\left( {x + 3} \right)\left( {x - 2} \right) \\
\ \]
Thus , the factors of the given polynomial are \[\left( {x - 1} \right)\left( {x + 3} \right)\left( {x - 2} \right)\]
Note: Factorization method is the process of factoring a polynomial into factors for which we use the several methods they are trial and error method, division method and the remainder theorem.
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE

What is the full form of pH?




