
Factorize: \[15x + 5\].
Answer
567k+ views
Hint:
The given expression is an algebraic expression. We will first factor out the common term from the given expression. Factorisation is the process to express a complex term in its simplest terms in the form of multiplication. We keep breaking a term into multiplication of two or three terms.
Complete step by step solution:
We need to factorise the given expression \[15x + 5\]. The first step in factorisation for algebraic equations are taking common parts out. It can be constants or variables or both.
In the given expression, 5 and 15 are constant and \[x\] is the only variable. We know that 15 is a multiple of 5.
Therefore, we will take 5 common expressions. As the variable is not present with both the constants, we will not consider it as a common term. Therefore, we get
\[15x + 5 = 5\left( {3x + 1} \right)\].
We expressed the term \[15x + 5\] in the multiplication form of 5 and \[3x + 1\]. No more factorisation of these two terms is possible.
Therefore, the factorisation of \[15x + 5\] is \[5\left( {3x + 1} \right)\].
Note:
The given expression is a linear expression. Linear expression is the expression where the variable has the highest power of 1. We can convert a linear expression into a linear equation by equating it to 0.
In factorization, for the constant parts we always take the H.C.F which is the highest common factor of the available constants. In this case 5 was the H.C.F of 5 and 15.
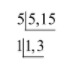
We also need to remember that the power of the variables in the factorised parts will always be less than or equal to the power of the main equation.
The given expression is an algebraic expression. We will first factor out the common term from the given expression. Factorisation is the process to express a complex term in its simplest terms in the form of multiplication. We keep breaking a term into multiplication of two or three terms.
Complete step by step solution:
We need to factorise the given expression \[15x + 5\]. The first step in factorisation for algebraic equations are taking common parts out. It can be constants or variables or both.
In the given expression, 5 and 15 are constant and \[x\] is the only variable. We know that 15 is a multiple of 5.
Therefore, we will take 5 common expressions. As the variable is not present with both the constants, we will not consider it as a common term. Therefore, we get
\[15x + 5 = 5\left( {3x + 1} \right)\].
We expressed the term \[15x + 5\] in the multiplication form of 5 and \[3x + 1\]. No more factorisation of these two terms is possible.
Therefore, the factorisation of \[15x + 5\] is \[5\left( {3x + 1} \right)\].
Note:
The given expression is a linear expression. Linear expression is the expression where the variable has the highest power of 1. We can convert a linear expression into a linear equation by equating it to 0.
In factorization, for the constant parts we always take the H.C.F which is the highest common factor of the available constants. In this case 5 was the H.C.F of 5 and 15.
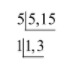
We also need to remember that the power of the variables in the factorised parts will always be less than or equal to the power of the main equation.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 7 English: Engaging Questions & Answers for Success

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE





