Question

Factorise the algebraic expression ${z^2} - z - 2$.

Answer 1

Hint: For factoring the given expression we have to find the roots or follow factorization process.
Method 1: FACTORIZATION: In this process we spit the z term into the sum of any two appropriate numbers whose product results in the constant value of the expression. From here we can simplify the rest of the expression.
Method2: GETTING ROOTS: In this method, we find the roots of the expression. We already know that for roots a, b the expression is $(x - a)(x - b)$ and its elaborate form is ${x^2} - (a + b)x + ab$.
Here in this question we take roots be a, b. As from the equation above we know the sum of roots and product of roots . We can get a-b from the formula
\[{(a - b)^2} = {(a + b)^2} - 4ab\]
Now from a + b and a – b we get the values of a and b and substitute them in $(x - a)(x - b)$.

Complete step-by-step solution:
METHOD 1: -z can be written as the sum of -2z and z.
${z^2} - z - 2 \\
= {z^2} - 2z + z - 2 \\
= z(z - 2) + (z - 2) \\
= (z + 1)(z - 2) $
Hence, ${z^2} - z - 2 = (z + 1)(z - 2)$.
METHOD 2 :
Let us consider the roots of expression ${z^2} - z - 2$ be a, b.
By comparison with ${x^2} - (a + b)x + ab$,
$a + b = 1 \\
ab = - 2 $
Then,
${(a - b)^2} = {(1)^2} - 4( - 2) \\
\Rightarrow {(a - b)^2} = 1 + 8 \\
\Rightarrow {(a - b)^2} = 9 \\
\Rightarrow a - b = 3 \\
\Rightarrow a = 3 + b $
Substitute the arrived value ‘a’ in a + b , we get
$a + b = 1 \\
\Rightarrow 3 + b + b = 1 \\
\Rightarrow 3 + 2b = 1 \\
\Rightarrow 2b = - 2 \\
\Rightarrow b = - 1 $
and
$ a = 3 + b \\
\Rightarrow a = 3 + ( - 1) \\
\Rightarrow a = 2 $
The expression
\[{z^2} - z - 2 \\
= (z - a)(z - b) \\
= (z - 2)(z - ( - 1)) \\
= (z - 2)(z + 1) \]

Note: The graph of expression ${z^2} - z - 2$ is

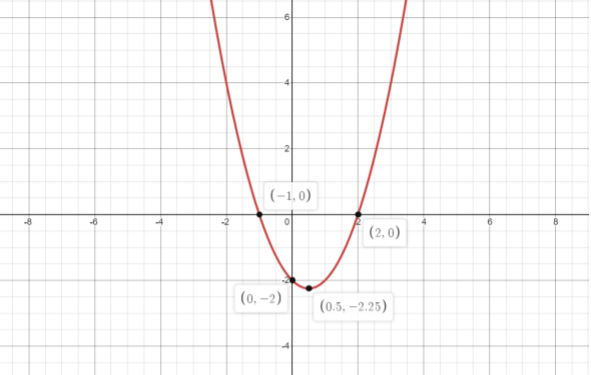
From the graph the roots are ( -1 , 0 ) , ( 2 , 0 ) . From the graph the minimum of the expression ${z^2} - z - 2$ is ( 0.5 , -2.25 ) . Graphical methods are another way to find the roots. The points where the curve intersects the X-axis are roots.