Question

How do you factor the trinomial $2{{x}^{2}}-32x+128$?

Answer 1

Hint: In this problem we need to calculate the factors of the given equation. We can observe that the given equation is a quadratic equation or trinomial equation. For calculating the factors first, we are going to calculate the roots of the given equation by using the quadratic formula $x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$. So, we will compare the given equation with the standard form of quadratic equation which is $a{{x}^{2}}+bx+c$ and note the values of $a$, $b$, $c$. After that we will use the formula to get the roots of the equation. Once we have the roots of the quadratic equation as $\alpha $, $\beta $ we can write the factors of the equation as $x-\alpha $, $x-\beta $.

Complete step by step solution:
Given that, $2{{x}^{2}}-32x+128$.
Comparing the above equation with $a{{x}^{2}}+bx+c$, then we will get
$a=2$, $b=-32$, $c=128$.
Now the roots of the given equation form the formula $x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$ are given by
$\Rightarrow x=\dfrac{-\left( -32 \right)\pm \sqrt{{{\left( -32 \right)}^{2}}-4\left( 2 \right)\left( 128 \right)}}{2\left( 2 \right)}$
Simplifying the above equation, then we will get
$\begin{align}
  & \Rightarrow x=\dfrac{32\pm \sqrt{1024-1024}}{4} \\
 & \Rightarrow x=\dfrac{32\pm 0}{4} \\
 & \Rightarrow x=\dfrac{32+0}{4}\text{ or }\dfrac{32-0}{4} \\
 & \Rightarrow x=8\text{ or }8 \\
\end{align}$
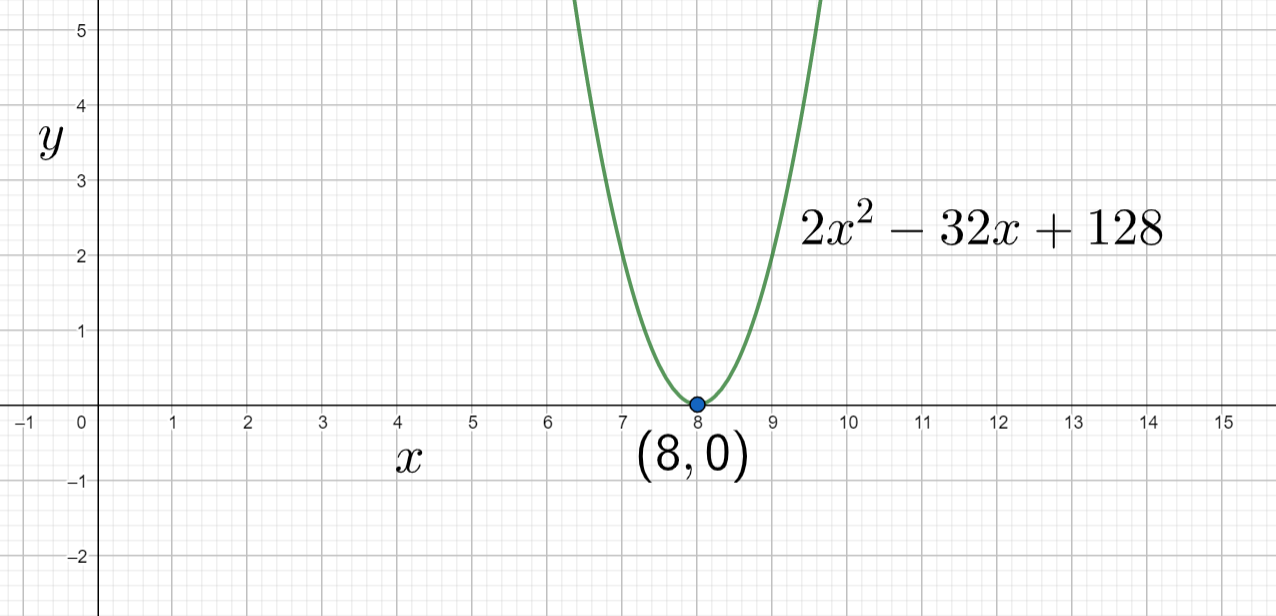
Here We have the roots as $8$, $8$. Hence the factors of the given equation are $x-8$, $x-8$. The graph of the given equation will be

Note: We can also directly find the factors by using the factorization method in which we will split the middle term according to the factors of the value $ac$. After that we will take appropriate terms as common from the equation and simplify it to get the factors.