Question

How many faces and edges does a triangular prism have?

Answer 1

Hint: Draw any triangular prism using the fact that a triangular prism is a three-sided prism. Count the number of its faces and vertices. Use the formula $f+v-e=2$, where f denotes the number of faces, v denotes the number of vertices and e denotes the number of edges, to count the number of vertices of the prism.

Complete step-by-step answer:
We have to find out the number of faces and edges of a triangular prism.

We know that a triangular prism is a three-sided prism. It’s a polyhedron made of 2 triangular bases and 3 rectangular faces joining sides.

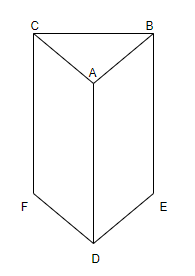
We observe that this triangular prism has 5 faces – 2 triangular bases and 3 rectangular faces joining sides. We observe that the triangular prism has 6 edges – A, B, C, D, E, and F.
We can now count the number of edges of the prism, or, we can use the formula $f+v-e=2$, where f denotes the number of faces, v denotes the number of vertices and e denotes the number of edges to count the number of vertices of the prism.
Substituting $f=5,v=6$ in the above formula, we have $5+6-e=2$.

Rearranging the terms, we have $e=11-2=9$.
Thus, the prism has 9 edges. We can also count these edges by looking at the prism.
Hence, the triangular prism has 5 faces and 9 edges.
Note: It’s difficult to count the number of edges on the prism from a diagram due to its 3 – D orientation. Thus, it’s better to use the relation given between the number of edges, vertices, and faces to count the number of edges of the prism.