Question

f a triangle and a square are on the same base and between the same parallel then the ratio of the area of the triangle to the area of the square is:
(a) 1:2
(b) 3:1
(c) 1:4
(d) 2:3

Answer 1

Hint: First of all, draw two equal parallels and make a square and triangle in between them with the same base. Now, use \[\dfrac{1}{2}\times base\times height\] to find the area of the triangle and \[{{\left( \text{side} \right)}^{2}}\] to find the area of the square and find their ratios.

Complete step-by-step answer:
In this question, we are given that if a triangle and a square are on the same base and between the same parallel then we have to find the ratio of the area of the triangle to the area of the square. Let us draw two equal parallels AB and CD.

Now, join A to B and B to C such that AB = BC = CD = DA = l, so that ABCD is a square.

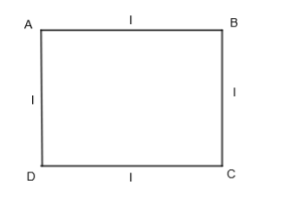
Also, now take E on the line AB and join C and D to make a triangle ECD with base CD and between the parallels AB and CD which is the same as that of the square.

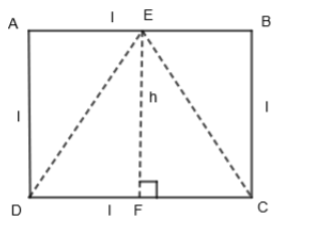
Now, let us find the area of the square ABCD. We know that the area of the square = \[{{\left( \text{side} \right)}^{2}}\]. So, by using this, we get,
Area of the square ABCD = \[{{\left( AB \right)}^{2}}\]. We know that AB = l. So, we get,
Area of the square ABCD = \[{{l}^{2}}....\left( i \right)\]
Now, let us find the area of the triangle ECD. We know that area of the triangle = \[\dfrac{1}{2}\times base\times height\]. So, by using this, we get,
\[\text{Area of }\Delta ECD=\dfrac{1}{2}\times CD\times EF\]
From the diagram, we get CD = l and EF = BC = l. By substituting these values in the above equation, we get,
\[\text{Area of }\Delta ECD=\dfrac{1}{2}\times l\times l=\dfrac{1}{2}{{l}^{2}}....\left( ii \right)\]
Now, by dividing equation (ii) with equation (i), we get,
\[\dfrac{\text{Area of }\Delta \text{ECD}}{\text{Area of the square ABCD}}=\dfrac{\dfrac{1}{2}{{l}^{2}}}{{{l}^{2}}}\]
By canceling the like terms from RHS of the above equation, we get,
\[\dfrac{\text{Area of }\Delta \text{ECD}}{\text{Area of the square ABCD}}=\dfrac{1}{2}\]
So, we get the ratio of the area of the triangle to the area of the square as 1:2.
Hence, option (a) is the right answer.

Note: In this question, students must note that we can locate the third vertex of the triangle, that is E at any point on line AB, our answer will remain the same in any case because AB is parallel to CD. So, the height of the triangle will remain constant irrespective of the position of the point E on the line AB. Also, students must remember that they must draw AB and CD initially equal and keep the same distance between them as well to make ABCD a square. Also, the diagram should be properly drawn.