Question

What is expression for Moment of inertia of a solid cylinder about its own axis of symmetry and about an axis perpendicular to its length $?$

Answer 1

Hint:To derive the expression for Moment of inertia of a solid cylinder about its axes, we make use of the theorem of parallel and perpendicular axes. Also, the concept of moment of inertia of a rigid body about the axis of rotation is used.

Formula used:
Moment of inertia is of a rigid body can be expressed as
$I = \int {{r^2}dm} $
Where, $r$ - perpendicular distance of particles in a rigid body from the axis of rotation.
$dm$ - infinitesimal small part of mass of the whole body situated at distance $r$.

Complete step by step answer:
About its own axis of symmetry, consider a solid cylinder of length $L$, mass $M$ having density $\rho $rotating about an axis passing through its own axis of symmetry. Let us consider the one end area of the cylinder which looks like a shell and the mass element of shell $dm$ in terms of infinitesimal radial thickness $dr$.

(i) Using, the general definition of Moment of inertia,
$I = \int_0^M {{r^2}dm} - - - - - - - - - - (1)$
The mass element can be expressed in terms of infinitesimal radial thickness $dr$by
$dm = \rho dV = \rho L2\pi rdr - - - - - - - - - - - (2)$
Here, $dV$ - volume element of the shell which is $dV = 2\pi rL$
Substituting the value of $dm$in eq$(1)$, we get
\[I = 2\pi \rho L\int_0^R {{r^3}dr} \]
Here, the change of limits of integration is due to substitution of $dr$in place of $dm$.
By solving, we get
\[I = 2\pi \rho L\dfrac{{{R^4}}}{4} - - - - - - - - - - (3)\]
Now, the density is given by $\rho = \dfrac{M}{V} = \dfrac{M}{{\pi {R^2}L}}$.
Substituting this in eq$(3)$, we get
\[I = 2\pi \left[ {\dfrac{M}{{\pi {R^2}L}}} \right]L\dfrac{{{R^4}}}{4}\]
\[\therefore I = \dfrac{1}{2}M{R^2}\]
This is the moment of inertia of a solid cylinder about its own axis of symmetry .

(ii) About an axis perpendicular to its length, consider the solid cylinder having mass $M$ , radius $R$, length $L$ and Z axis passing through the central axis of the cylinder.

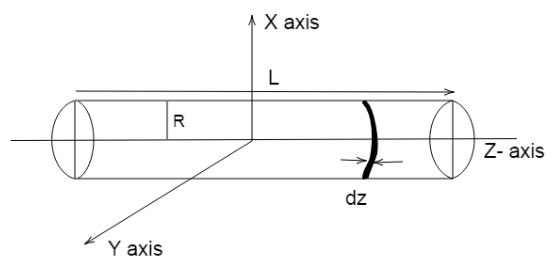
Let the moment of inertia of cylinder infinitesimally thin disks with thickness $dz$ .
$dm = \rho \times V$
$\Rightarrow dm = \dfrac{M}{V} \times (\pi {r^2}dz)$
$\Rightarrow dm = \dfrac{M}{{\pi {r^2}L}} \times (\pi {r^2}dz)$
Thus, $dm = \dfrac{M}{L}dz - - - - - - - - - - - - (1)$
The moment of inertia about central axis is,
\[{I_Z} = \dfrac{1}{2}{R^2}dm\]
Now, Using the theorem of perpendicular axes, we have
$d{I_Z} = d{I_X} + d{I_Y}$
Here, both X and Y moments of inertia are equal by symmetry, and hence
$d{I_X} = \dfrac{{d{I_Z}}}{2} - - - - - - - - - - (2)$

Substituting from above equation, we get
$d{I_X} = \dfrac{1}{2} \times \left[ {\dfrac{1}{2}{R^2}dm} \right]$
\\Rightarrow d{I_X} = \dfrac{1}{4}{R^2}dm - - - - - - - - - - - - (3)\]
Also, for X-axis, we make use of theorem of parallel axis, then
\[d{I_X} = \dfrac{1}{4}{R^2}dm + {z^2}dm - - - - - - - - - - - - (4)\]
Now, Conducting the integration over the length of solid cylinder from $z = 0$ to $z = L$,
${I_X} = \int_0^L {d{I_X}} $
\[\Rightarrow {I_X} = \int_0^L {\dfrac{1}{4}\dfrac{M}{L}{R^2}dz + } \int_0^L {{z^2}} \dfrac{M}{L}dz\]
By solving, and ignoring the constants, we get
\[{I_X} = \dfrac{1}{4}\dfrac{M}{L}{R^2}L + \dfrac{{M{L^2}}}{3}\]
$\therefore {I_X} = \dfrac{1}{4}M{R^2} + \dfrac{{M{L^2}}}{3}$
This is the expression for moment of inertia of a solid cylinder about an axis passing through its centre and perpendicular to its length.

Note: We should be familiar with integration over the surface within the limits. We must know about the theorem of parallel and perpendicular axes about an axis of rotation.Moment of inertia is defined as the quantity expressed by the body resisting angular acceleration which is the sum of the product of the mass of every particle with its square of a distance from the axis of rotation.