Question

How to express these vectors in terms of $p$ and $q$. ABCDEF is a regular hexagon with centre O. Suppose$\overrightarrow {AB} = \overrightarrow p $ and $\overrightarrow {AF} = \overrightarrow q $, express \[\overrightarrow {AO,} \overrightarrow {AC} ,\overrightarrow {AE} ,\overrightarrow {CE} \] in terms of $\overrightarrow p $ and $\overrightarrow q $

Answer 1

Hint: In this question we are asked to express vectors, in a regular hexagon. In order to proceed with this question we need to know about vectors and hexagons. Hexagon is a polygon which has six sides and six angles. Regular hexagons have all the six sides and six angles equal, whereas irregular hexagons do not have all the sides and angles equal. Regular hexagons can also be represented as six equilateral triangles arranged together. All the interior angles add up to ${720^ \circ }$ and all the exterior angles add up to ${360^ \circ }$. Vectors are the quantities which have a direction along with magnitude. They are used to calculate quantities like force.

Complete step by step solution:
We are given,

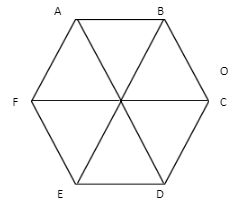
$\overrightarrow {AB} = \overrightarrow p $
$\overrightarrow {AF} = \overrightarrow q $
Since it is a regular hexagon, all the sides of the hexagon are of equal length.
$ \Rightarrow \overrightarrow {AB} = \overrightarrow {BC} = \overrightarrow {CD} = \overrightarrow {DE} = \overrightarrow {EF} = \overrightarrow p $
$ \Rightarrow \overrightarrow {AF} = \overrightarrow {FE} = \overrightarrow {ED} = \overrightarrow {DC} = \overrightarrow {CB} = \overrightarrow {BA} = \overrightarrow q $
$ \Rightarrow \overrightarrow p = - \overrightarrow q $
Since a hexagon has \[4 \times {180^o}\; = {\text{ }}{720^o}\], each angle in a regular hexagon is \[\dfrac{{{{720}^o}}}{6}{\text{ }} = {\text{ }}{120^o}\]. When we bisect them we get \[{60^o}\]angles. Since each triangle has two \[{60^o}\] angles, they are all equilateral triangles.
So,
$ \Rightarrow \overrightarrow {AO} = \overrightarrow {BO} = \overrightarrow {CO} = \overrightarrow {DO} = \overrightarrow {EO} = \overrightarrow {FO} $
\[ \Rightarrow \overrightarrow {AO} = \overrightarrow p = - \overrightarrow q \]
\[
   \Rightarrow \overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow p + \overrightarrow p = 2\overrightarrow p \;\;\;\;\;\left( {Using{\text{ }}vector{\text{ }}law{\text{ }}of{\text{ }}addition} \right) \\
   \Rightarrow \overrightarrow {AC} = \overrightarrow {AF} + \overrightarrow {FE} + \overrightarrow {ED} + \overrightarrow {DC} = \overrightarrow q + \overrightarrow q + \overrightarrow q + \overrightarrow q = 4\overrightarrow q \;
 \]
\[
   \Rightarrow \overrightarrow {CE} = \overrightarrow {CD} + \overrightarrow {DE} = \overrightarrow p + \overrightarrow p = 2\overrightarrow p \;\;\;\;\;\left( {Using{\text{ }}vector{\text{ }}law{\text{ }}of{\text{ }}addition} \right) \\
   \Rightarrow \overrightarrow {CE} = \overrightarrow {CB} + \overrightarrow {BA} + \overrightarrow {AF} + \overrightarrow {FE} = \overrightarrow q + \overrightarrow q + \overrightarrow q + \overrightarrow q = 4\overrightarrow q \\
 \]
\[
   \Rightarrow \overrightarrow {AE} = \overrightarrow {AF} + \overrightarrow {FE} = \overrightarrow q + \overrightarrow q = 2\overrightarrow q \;\;\;\;\;\left( {Using{\text{ }}vector{\text{ }}law{\text{ }}of{\text{ }}addition} \right) \\
   \Rightarrow \overrightarrow {AE} = \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DE} = \overrightarrow p + \overrightarrow p + \overrightarrow p + \overrightarrow p = 2\overrightarrow p \;
 \]
Formula used: Vector Law of addition
To obtain $\overrightarrow R $ which is the resultant of the sum of vectors $\overrightarrow A $ and $\overrightarrow B $ with the same order of magnitude and direction as shown in the figure, we use the following rule:
$\overrightarrow R = \overrightarrow A + \overrightarrow B $

Note: Vectors are represented with an arrow sign above the magnitude, which represents direction. For example, quantities like displacement need direction as well. Magnitude of a vector cannot be negative, it is always positive. But the vector which has the same magnitude but opposite direction is represented by a negative vector. Vector without direction is known as a scalar.