Question

Express the trigonometric ratio $\tan A$ in terms of $\sec A$.

Answer 1

Hint: Consider a right-angled triangle; $\angle B = {90^ \circ }$, then $BC$ is perpendicular, $AB$ is base and $AC$ is hypotenuse.

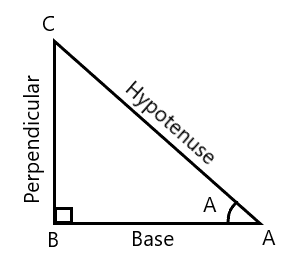
Then, $6$ ratios (trigonometric ratio) are $\operatorname{Sin} A = \dfrac{P}{H}$, $\operatorname{Cos} A = \dfrac{B}{H}$, $\operatorname{Tan} A = \dfrac{P}{B}$, $\operatorname{Cos} ecA = \dfrac{H}{P}$, $\operatorname{Sec} A = \dfrac{H}{B}$, $CotA = \dfrac{B}{P}$. Also, we will be using the identity: $1 + {\tan ^2}A = {\operatorname{Sec} ^2}A$

Complete step-by-step answer:
Here, we have to express $\tan A$ in terms of $\sec A$.
We have three basic formulas for converting some trigonometric ratio into one another. Here are the $3$ formulas:
$1 + {\tan ^2}\theta = {\sec ^2}\theta .........(1)$
${\sec ^2}\theta + {\cos ^2}\theta = 1.........(2)$
$1 + {\cot ^2}\theta = \cos e{c^2}\theta {\text{ }}........(3)$
These three formulas are related to each other after squaring means ${\tan ^2}\theta $ not $\tan \theta $.
We want to express $\tan A$ in terms of $\sec A$.
Therefore, using the identity (1):
$1 + {\tan ^2}A = \sec A$
Here, ‘$A$’ is the angle which is given and therefore, we replaced $A$ with $\theta $.
We have to express $\tan A$ in $\sec A$, So we need to keep $\tan A$ in left hand side and moving rest of the terms to right hand side, we get:
${\tan ^2}A = {\sec ^2}A - 1$
Now, we have an extra square of $\tan A$.
Therefore, to get rid of this square, we took square root on both sides that is L.H.S and R.H.S
$\sqrt {{{\tan }^2}A} = \sqrt {{{\sec }^2}A - 1} $
Square root and square cancels each other

Therefore, $\tan A = \sqrt {{{\sec }^2}A - 1} $

Note: Trigonometric ratio includes some of the following formulas: $\cos ecA = \dfrac{1}{{\sin A}}$, $\sin A = \dfrac{1}{{\cos ecA}}$, $\cos A = \dfrac{1}{{\sec A}}$, $\sec A = \dfrac{1}{{\cos A}}$, $\tan A = \dfrac{1}{{\cot A}}$, $\cot A = \dfrac{1}{{\tan A}}$. Also, we have: $\tan A = \dfrac{{\sin A}}{{\cos A}}$ and $\cot A = \dfrac{{\cos A}}{{\sin A}}$
By using these formulas of trigonometric ratio, We can convert one trigonometric ratio into another one and vice-versa. Also, the inverse of trigonometric ratios exists.