Express the following degrees into their corresponding radians:
(i) ${{110}^{\circ }}30'$
(ii) ${{845}^{\circ }}25'35''$
Answer
Verified596.4k+ views
Hint: We will apply here the relation between radians and degrees. This relation has a numerical form which is given by ${{\left( \pi \right)}^{c}}={{180}^{\circ }}$. This can also be written as ${{\left( \dfrac{\pi }{180} \right)}^{c}}={{\left( 1 \right)}^{\circ }}$ after dividing the equation by ${{180}^{\circ }}$.
Complete step-by-step answer:
The diagram showing degree and radians together inside a circle is shown below.
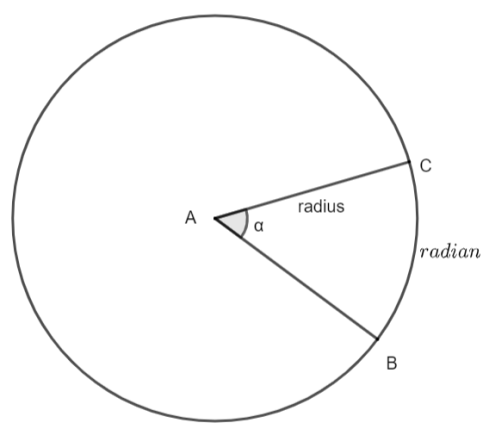
In the diagram AC and AB are the radiuses of the circle. The radian is an arc which is formed by two radiuses in a circle joining together at point A. In this figure the radian is represented by an arc BC. The is called an angle made by the two radiuses intersecting at point A. In the figure the angle is represented by $\angle BAC=\alpha $. Now, the relation between radians and degree is given by by ${{\left( \pi \right)}^{c}}={{180}^{\circ }}$. This can also be written as ${{\left( \dfrac{\pi }{180} \right)}^{c}}={{\left( 1 \right)}^{\circ }}$ after dividing the equation by ${{180}^{\circ }}$.
Now, we will consider the degree ${{110}^{\circ }}30'$ and we will find its value in radian. As we know that one degree is divided into 60 minutes of an arc therefore, we have ${{\left( 1 \right)}^{\circ }}=60'$ or, ${{\left( \dfrac{1}{60} \right)}^{\circ }}=1'$. Thus, we now have
$\begin{align}
& {{110}^{\circ }}30'={{110}^{\circ }}+30' \\
& \Rightarrow {{110}^{\circ }}30'={{110}^{\circ }}+\left( 30\times 1' \right) \\
& \Rightarrow {{110}^{\circ }}30'={{110}^{\circ }}+\left( 30\times {{\left( \dfrac{1}{60} \right)}^{\circ }} \right) \\
& \Rightarrow {{110}^{\circ }}30'={{110}^{\circ }}+\left( {{\left( 30\times \dfrac{1}{60} \right)}^{\circ }} \right) \\
& \Rightarrow {{110}^{\circ }}30'={{110}^{\circ }}+{{\left( \dfrac{1}{2} \right)}^{\circ }} \\
& \Rightarrow {{110}^{\circ }}30'={{\left( 110+\dfrac{1}{2} \right)}^{\circ }} \\
& \Rightarrow {{110}^{\circ }}30'={{\left( \dfrac{220+1}{2} \right)}^{\circ }} \\
& \Rightarrow {{110}^{\circ }}30'={{\left( \dfrac{221}{2} \right)}^{\circ }} \\
\end{align}$
Now we will apply the formula ${{\left( \dfrac{\pi }{180} \right)}^{c}}={{\left( 1 \right)}^{\circ }}$. Therefore, we have ${{\left( \dfrac{221}{2} \right)}^{\circ }}=\dfrac{221}{2}\times {{\left( 1 \right)}^{\circ }}$. By substituting the value of ${{\left( 1 \right)}^{\circ }}$ we will have,
$\begin{align}
& {{\left( \dfrac{221}{2} \right)}^{\circ }}=\dfrac{221}{2}\times {{\left( 1 \right)}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{221}{2} \right)}^{\circ }}=\dfrac{221}{2}\times {{\left( \dfrac{\pi }{180} \right)}^{c}} \\
& \Rightarrow {{\left( \dfrac{221}{2} \right)}^{\circ }}={{\left( \dfrac{221}{2}\times \dfrac{\pi }{180} \right)}^{c}} \\
& \Rightarrow {{\left( \dfrac{221}{2} \right)}^{\circ }}={{\left( \dfrac{221\pi }{360} \right)}^{c}} \\
\end{align}$
Now we will consider the degree ${{845}^{\circ }}25'35''$ and find its corresponding radian. As we know that one degree is divided into 60 minutes of an arc therefore, we have ${{\left( 1 \right)}^{\circ }}=60'$ or, ${{\left( \dfrac{1}{60} \right)}^{\circ }}=1'$. Also, 1 minute is equal to 3600 seconds which is written as,
$\begin{align}
& {{\left( 1 \right)}^{\prime \prime }}={{\left( \dfrac{1}{60\times 60} \right)}^{\circ }} \\
& \Rightarrow {{\left( 1 \right)}^{\prime \prime }}={{\left( \dfrac{1}{3600} \right)}^{\circ }} \\
\end{align}$
Thus, we now have
$\begin{align}
& {{845}^{\circ }}25'3{5}''={{845}^{\circ }}+25'+3{5}'' \\
& \Rightarrow {{845}^{\circ }}25'3{5}''={{845}^{\circ }}+\left( 25\times \left( 1 \right)' \right)+\left( 35\times {{\left( 1 \right)}^{\prime \prime }} \right) \\
& \Rightarrow {{845}^{\circ }}25'3{5}''={{845}^{\circ }}+\left( 25\times {{\left( \dfrac{1}{60} \right)}^{\circ }} \right)+\left( 35\times {{\left( \dfrac{1}{3600} \right)}^{\circ }} \right) \\
& \Rightarrow {{845}^{\circ }}25'3{5}''={{845}^{\circ }}+{{\left( \dfrac{25}{60} \right)}^{\circ }}+{{\left( \dfrac{35}{3600} \right)}^{\circ }} \\
& \Rightarrow {{845}^{\circ }}25'3{5}''={{845}^{\circ }}+{{\left( \dfrac{5}{12} \right)}^{\circ }}+{{\left( \dfrac{7}{720} \right)}^{\circ }} \\
\end{align}$
As we know that the l.c.m. of 1, 12 and 720 is 720. Thus, we get
$\begin{align}
& \Rightarrow {{845}^{\circ }}25'3{5}''={{845}^{\circ }}+{{\left( \dfrac{5}{12} \right)}^{\circ }}+{{\left( \dfrac{7}{720} \right)}^{\circ }} \\
& \Rightarrow {{845}^{\circ }}25'3{5}''={{\left( \dfrac{608400+60+7}{720} \right)}^{\circ }} \\
& \Rightarrow {{845}^{\circ }}25'3{5}''={{\left( \dfrac{608467}{720} \right)}^{\circ }} \\
\end{align}$
Now we will apply the formula ${{\left( \dfrac{\pi }{180} \right)}^{c}}={{\left( 1 \right)}^{\circ }}$. Therefore, we have $\dfrac{608467}{720}\times {{\left( 1 \right)}^{\circ }}$. By substituting the value of ${{\left( 1 \right)}^{\circ }}$ we will have,
$\begin{align}
& {{845}^{\circ }}25'3{5}''=\dfrac{608467}{720}\times {{\left( 1 \right)}^{\circ }} \\
& \Rightarrow {{845}^{\circ }}25'3{5}''=\dfrac{608467}{720}\times {{\left( \dfrac{\pi }{180} \right)}^{c}} \\
& \Rightarrow {{845}^{\circ }}25'3{5}''={{\left( \dfrac{608467}{720}\times \dfrac{\pi }{180} \right)}^{c}} \\
& \Rightarrow {{845}^{\circ }}25'3{5}''={{\left( \dfrac{608467\pi }{129600} \right)}^{c}} \\
\end{align}$
Hence, the degree ${{110}^{\circ }}30'$ is equal to ${{\left( \dfrac{221\pi }{360} \right)}^{c}}$ in radian and the degree ${{845}^{\circ }}25'3{5}''$ is equal to ${{\left( \dfrac{608467\pi }{129600} \right)}^{c}}$.
Note: If we were asked to find the value in pure radian form without $\pi $ then we can solve it with the substitution as $\pi =\dfrac{22}{7}$. Therefore, we have
$\begin{align}
& {{110}^{\circ }}30'={{\left( \dfrac{221\pi }{360} \right)}^{c}} \\
& \Rightarrow {{110}^{\circ }}30'=\left( \dfrac{221}{360}\times \dfrac{22}{7} \right) \\
& \Rightarrow {{110}^{\circ }}30'={{\left( \dfrac{2431}{1260} \right)}^{c}} \\
& \Rightarrow {{110}^{\circ }}30'={{\left( 1.92 \right)}^{c}} \\
\end{align}$
Alternatively, we can substitute the direct value of ${{\left( 1 \right)}^{\circ }}={{\left( 0.0174 \right)}^{c}}$ in the expression $\begin{align}
& {{110}^{\circ }}30'={{\left( \dfrac{221}{2} \right)}^{\circ }} \\
& \Rightarrow {{110}^{\circ }}30'=\dfrac{221}{2}\times {{\left( 1 \right)}^{\circ }} \\
& \Rightarrow {{110}^{\circ }}30'=\dfrac{221}{2}\times {{\left( 0.0174 \right)}^{c}} \\
& \Rightarrow {{110}^{\circ }}30'={{\left( \dfrac{221}{2}\times 0.0174 \right)}^{c}} \\
& \Rightarrow {{110}^{\circ }}30'={{\left( 1.9227 \right)}^{c}} \\
\end{align}$
Similarly we can apply the same procedure to ${{845}^{\circ }}25'35''$.
Complete step-by-step answer:
The diagram showing degree and radians together inside a circle is shown below.
In the diagram AC and AB are the radiuses of the circle. The radian is an arc which is formed by two radiuses in a circle joining together at point A. In this figure the radian is represented by an arc BC. The is called an angle made by the two radiuses intersecting at point A. In the figure the angle is represented by $\angle BAC=\alpha $. Now, the relation between radians and degree is given by by ${{\left( \pi \right)}^{c}}={{180}^{\circ }}$. This can also be written as ${{\left( \dfrac{\pi }{180} \right)}^{c}}={{\left( 1 \right)}^{\circ }}$ after dividing the equation by ${{180}^{\circ }}$.
Now, we will consider the degree ${{110}^{\circ }}30'$ and we will find its value in radian. As we know that one degree is divided into 60 minutes of an arc therefore, we have ${{\left( 1 \right)}^{\circ }}=60'$ or, ${{\left( \dfrac{1}{60} \right)}^{\circ }}=1'$. Thus, we now have
$\begin{align}
& {{110}^{\circ }}30'={{110}^{\circ }}+30' \\
& \Rightarrow {{110}^{\circ }}30'={{110}^{\circ }}+\left( 30\times 1' \right) \\
& \Rightarrow {{110}^{\circ }}30'={{110}^{\circ }}+\left( 30\times {{\left( \dfrac{1}{60} \right)}^{\circ }} \right) \\
& \Rightarrow {{110}^{\circ }}30'={{110}^{\circ }}+\left( {{\left( 30\times \dfrac{1}{60} \right)}^{\circ }} \right) \\
& \Rightarrow {{110}^{\circ }}30'={{110}^{\circ }}+{{\left( \dfrac{1}{2} \right)}^{\circ }} \\
& \Rightarrow {{110}^{\circ }}30'={{\left( 110+\dfrac{1}{2} \right)}^{\circ }} \\
& \Rightarrow {{110}^{\circ }}30'={{\left( \dfrac{220+1}{2} \right)}^{\circ }} \\
& \Rightarrow {{110}^{\circ }}30'={{\left( \dfrac{221}{2} \right)}^{\circ }} \\
\end{align}$
Now we will apply the formula ${{\left( \dfrac{\pi }{180} \right)}^{c}}={{\left( 1 \right)}^{\circ }}$. Therefore, we have ${{\left( \dfrac{221}{2} \right)}^{\circ }}=\dfrac{221}{2}\times {{\left( 1 \right)}^{\circ }}$. By substituting the value of ${{\left( 1 \right)}^{\circ }}$ we will have,
$\begin{align}
& {{\left( \dfrac{221}{2} \right)}^{\circ }}=\dfrac{221}{2}\times {{\left( 1 \right)}^{\circ }} \\
& \Rightarrow {{\left( \dfrac{221}{2} \right)}^{\circ }}=\dfrac{221}{2}\times {{\left( \dfrac{\pi }{180} \right)}^{c}} \\
& \Rightarrow {{\left( \dfrac{221}{2} \right)}^{\circ }}={{\left( \dfrac{221}{2}\times \dfrac{\pi }{180} \right)}^{c}} \\
& \Rightarrow {{\left( \dfrac{221}{2} \right)}^{\circ }}={{\left( \dfrac{221\pi }{360} \right)}^{c}} \\
\end{align}$
Now we will consider the degree ${{845}^{\circ }}25'35''$ and find its corresponding radian. As we know that one degree is divided into 60 minutes of an arc therefore, we have ${{\left( 1 \right)}^{\circ }}=60'$ or, ${{\left( \dfrac{1}{60} \right)}^{\circ }}=1'$. Also, 1 minute is equal to 3600 seconds which is written as,
$\begin{align}
& {{\left( 1 \right)}^{\prime \prime }}={{\left( \dfrac{1}{60\times 60} \right)}^{\circ }} \\
& \Rightarrow {{\left( 1 \right)}^{\prime \prime }}={{\left( \dfrac{1}{3600} \right)}^{\circ }} \\
\end{align}$
Thus, we now have
$\begin{align}
& {{845}^{\circ }}25'3{5}''={{845}^{\circ }}+25'+3{5}'' \\
& \Rightarrow {{845}^{\circ }}25'3{5}''={{845}^{\circ }}+\left( 25\times \left( 1 \right)' \right)+\left( 35\times {{\left( 1 \right)}^{\prime \prime }} \right) \\
& \Rightarrow {{845}^{\circ }}25'3{5}''={{845}^{\circ }}+\left( 25\times {{\left( \dfrac{1}{60} \right)}^{\circ }} \right)+\left( 35\times {{\left( \dfrac{1}{3600} \right)}^{\circ }} \right) \\
& \Rightarrow {{845}^{\circ }}25'3{5}''={{845}^{\circ }}+{{\left( \dfrac{25}{60} \right)}^{\circ }}+{{\left( \dfrac{35}{3600} \right)}^{\circ }} \\
& \Rightarrow {{845}^{\circ }}25'3{5}''={{845}^{\circ }}+{{\left( \dfrac{5}{12} \right)}^{\circ }}+{{\left( \dfrac{7}{720} \right)}^{\circ }} \\
\end{align}$
As we know that the l.c.m. of 1, 12 and 720 is 720. Thus, we get
$\begin{align}
& \Rightarrow {{845}^{\circ }}25'3{5}''={{845}^{\circ }}+{{\left( \dfrac{5}{12} \right)}^{\circ }}+{{\left( \dfrac{7}{720} \right)}^{\circ }} \\
& \Rightarrow {{845}^{\circ }}25'3{5}''={{\left( \dfrac{608400+60+7}{720} \right)}^{\circ }} \\
& \Rightarrow {{845}^{\circ }}25'3{5}''={{\left( \dfrac{608467}{720} \right)}^{\circ }} \\
\end{align}$
Now we will apply the formula ${{\left( \dfrac{\pi }{180} \right)}^{c}}={{\left( 1 \right)}^{\circ }}$. Therefore, we have $\dfrac{608467}{720}\times {{\left( 1 \right)}^{\circ }}$. By substituting the value of ${{\left( 1 \right)}^{\circ }}$ we will have,
$\begin{align}
& {{845}^{\circ }}25'3{5}''=\dfrac{608467}{720}\times {{\left( 1 \right)}^{\circ }} \\
& \Rightarrow {{845}^{\circ }}25'3{5}''=\dfrac{608467}{720}\times {{\left( \dfrac{\pi }{180} \right)}^{c}} \\
& \Rightarrow {{845}^{\circ }}25'3{5}''={{\left( \dfrac{608467}{720}\times \dfrac{\pi }{180} \right)}^{c}} \\
& \Rightarrow {{845}^{\circ }}25'3{5}''={{\left( \dfrac{608467\pi }{129600} \right)}^{c}} \\
\end{align}$
Hence, the degree ${{110}^{\circ }}30'$ is equal to ${{\left( \dfrac{221\pi }{360} \right)}^{c}}$ in radian and the degree ${{845}^{\circ }}25'3{5}''$ is equal to ${{\left( \dfrac{608467\pi }{129600} \right)}^{c}}$.
Note: If we were asked to find the value in pure radian form without $\pi $ then we can solve it with the substitution as $\pi =\dfrac{22}{7}$. Therefore, we have
$\begin{align}
& {{110}^{\circ }}30'={{\left( \dfrac{221\pi }{360} \right)}^{c}} \\
& \Rightarrow {{110}^{\circ }}30'=\left( \dfrac{221}{360}\times \dfrac{22}{7} \right) \\
& \Rightarrow {{110}^{\circ }}30'={{\left( \dfrac{2431}{1260} \right)}^{c}} \\
& \Rightarrow {{110}^{\circ }}30'={{\left( 1.92 \right)}^{c}} \\
\end{align}$
Alternatively, we can substitute the direct value of ${{\left( 1 \right)}^{\circ }}={{\left( 0.0174 \right)}^{c}}$ in the expression $\begin{align}
& {{110}^{\circ }}30'={{\left( \dfrac{221}{2} \right)}^{\circ }} \\
& \Rightarrow {{110}^{\circ }}30'=\dfrac{221}{2}\times {{\left( 1 \right)}^{\circ }} \\
& \Rightarrow {{110}^{\circ }}30'=\dfrac{221}{2}\times {{\left( 0.0174 \right)}^{c}} \\
& \Rightarrow {{110}^{\circ }}30'={{\left( \dfrac{221}{2}\times 0.0174 \right)}^{c}} \\
& \Rightarrow {{110}^{\circ }}30'={{\left( 1.9227 \right)}^{c}} \\
\end{align}$
Similarly we can apply the same procedure to ${{845}^{\circ }}25'35''$.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success
Master Class 12 Biology: Engaging Questions & Answers for Success
Master Class 12 Chemistry: Engaging Questions & Answers for Success
Class 12 Question and Answer - Your Ultimate Solutions Guide
Complete reduction of benzene diazonium chloride with class 12 chemistry CBSE
How can you identify optical isomers class 12 chemistry CBSE
Trending doubts
Full form of STD, ISD and PCO
Convert 40circ C to Fahrenheit A 104circ F B 107circ class 8 maths CBSE
What is the difference between rai and mustard see class 8 biology CBSE
When people say No pun intended what does that mea class 8 english CBSE
What are the methods of reducing friction. Explain
Write a letter to the Municipal Commissioner to inform class 8 english CBSE