Question

How do you express $\sin \left( {{{\sin }^{ - 1}}\left( x \right) + {{\cos }^{ - 1}}\left( y \right)} \right)$ without trigonometric function?

Answer 1

Hint:Here, in the given question, we need to express $\sin \left( {{{\sin }^{ - 1}}\left( x \right) + {{\cos }^{ - 1}}\left( y \right)} \right)$ without trigonometric function. As we can see $\sin \left( {{{\sin }^{ - 1}}\left( x \right) + {{\cos }^{ - 1}}\left( y \right)} \right)$ is given in the form of an identity $\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin B$, so we will try to expand the given expression using this identity. After that we will use Pythagoras theorem to express functions in the form which is without any trigonometric function to get our required answer.

Formulae used:
$\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin B$
$\Rightarrow \sin \left( {{{\sin }^{ - 1}}x} \right) = x$
$\Rightarrow \cos \left( {{{\cos }^{ - 1}}y} \right) = y$

Complete step by step answer:
Given, $\sin \left( {{{\sin }^{ - 1}}\left( x \right) + {{\cos }^{ - 1}}\left( y \right)} \right)$
As we know, $\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin B$
Let $A = {\sin ^{ - 1}}x$ and $B = {\cos ^{ - 1}}y$.
$ \Rightarrow \sin \left( {{{\sin }^{ - 1}}x + {{\cos }^{ - 1}}y} \right) = \sin \left( {{{\sin }^{ - 1}}x} \right)\cos \left( {{{\cos }^{ - 1}}y} \right) + \cos \left( {{{\sin }^{ - 1}}x} \right)\sin \left( {{{\cos }^{ - 1}}y} \right)$
As we know, $\sin \left( {{{\sin }^{ - 1}}x} \right) = x$ and $\cos \left( {{{\cos }^{ - 1}}y} \right) = y$. Therefore, we get
$ \Rightarrow \sin \left( {{{\sin }^{ - 1}}x + {{\cos }^{ - 1}}y} \right) = xy + \cos \left( {{{\sin }^{ - 1}}x} \right)\sin \left( {{{\cos }^{ - 1}}y} \right).....\left( i \right)$
Now, we will solve $\cos \left( {{{\sin }^{ - 1}}x} \right)$ and $\sin \left( {{{\cos }^{ - 1}}y} \right)$ individually.
We have to find the value of $\cos \left( {{{\sin }^{ - 1}}x} \right) = \cos \left( {{{\sin }^{ - 1}}\dfrac{x}{1}} \right)$. As we know $\sin \theta = \dfrac{P}{H}$, from here we will find the value of base.
The right triangle with perpendicular = $x$ and hypotenuse = $1$. Therefore,

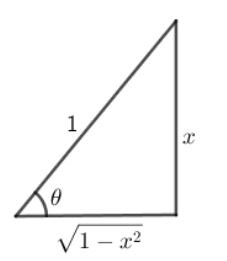
$Base = \sqrt {{H^2} - {P^2}} $
Base = $\sqrt {1 - {x^2}} $.
Therefore, we get
$ \Rightarrow {\sin ^{ - 1}}x = {\cos ^{ - 1}}\dfrac{{\sqrt {1 - {x^2}} }}{1}$.
Hence, $\cos \left( {{{\sin }^{ - 1}}x} \right) = \cos \left( {{{\cos }^{ - 1}}\dfrac{{\sqrt {1 - {x^2}} }}{1}} \right)$
$ \Rightarrow \cos \left( {{{\sin }^{ - 1}}x} \right) = \sqrt {1 - {x^2}} $
Now, we will find the value of $\sin \left( {{{\cos }^{ - 1}}y} \right) = \sin \left( {{{\cos }^{ - 1}}\dfrac{y}{1}} \right)$. As we know $\cos \theta = \dfrac{B}{H}$, from here we will find the value of perpendicular.
The right triangle with base = $y$ and hypotenuse = $1$. Therefore,

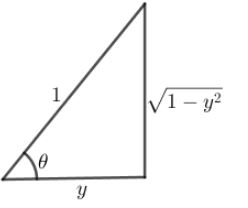
$Perpendicular = \sqrt {{H^2} - {B^2}} $
Perpendicular = $\sqrt {1 - {y^2}} $
Therefore, we get
$ \Rightarrow {\cos ^{ - 1}}y = {\sin ^{ - 1}}\dfrac{{\sqrt {1 - {y^2}} }}{1}$.
Hence, $\sin \left( {{{\cos }^{ - 1}}x} \right) = \sin \left( {{{\sin }^{ - 1}}\dfrac{{\sqrt {1 - {y^2}} }}{1}} \right)$
$ \Rightarrow \sin \left( {{{\cos }^{ - 1}}x} \right) = \sqrt {1 - {y^2}} $
Now, we will substitute value of $\cos \left( {{{\sin }^{ - 1}}x} \right)$ and $\sin \left( {{{\cos }^{ - 1}}y} \right)$ in $\left( i \right)$.
$\sin \left( {{{\sin }^{ - 1}}x + {{\cos }^{ - 1}}y} \right) = xy + \cos \left( {{{\sin }^{ - 1}}x} \right)\sin \left( {{{\cos }^{ - 1}}y} \right).....\left( i \right)$
$ \Rightarrow \sin \left( {{{\sin }^{ - 1}}x + {{\cos }^{ - 1}}y} \right) = xy + \sqrt {1 - {x^2}} \times \sqrt {1 - {y^2}} $

Therefore, we can write $\sin \left( {{{\sin }^{ - 1}}\left( x \right) + {{\cos }^{ - 1}}\left( y \right)} \right)$ without trigonometric functions as $xy + \sqrt {1 - {x^2}} \times \sqrt {1 - {y^2}} $.

Note:Remember that inverse trigonometric functions do the opposite of the regular trigonometric functions. For example: inverse $\sin e$ i.e., ${\sin ^{ - 1}}$ does the opposite of sine. The expression ${\sin ^{ - 1}}x$ is not the same as $\dfrac{1}{{\sin x}}$. In other words, the $ - 1$ is not an exponent. Instead, it simply means inverse function.