
Explain why the \[Be{H_2}\] molecule has a zero dipole moment although the $Be - H$ Bonds are polar.
Answer
582.3k+ views
Hint: Dipole moment is the product of magnitude of the partial charges developed on any covalently bonded atoms and the distance between the two atoms. Polar molecules are molecules in which distribution of charge between the covalently bonded atoms is not even due to the difference in the electro-negativity between the two bonded atoms.
Complete step by step answer:
We already know about the dipole moment. Polarity causes a molecule to have a dipole moment. There are some important points about dipole moment-
-In the case of polyatomic molecules the dipole moment not only depends upon the individual bonds but also on the spatial arrangement of various bonds in the molecule.
In such a case a molecule will have a dipole moment if the summation of all of the individual dipole moments is non-zero.
-Now, we know that in \[Be{H_2}\]molecule beryllium is the central atom which has no lone pair of electrons, only two bond pairs in its valence shell. These pairs form a covalent bond with two hydrogen atoms and the structure we obtain is linear which is given as-$H - Be - H$ .
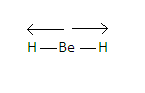
-Now we know that $Be - H$ Bond is polar as partial positive charge develops on hydrogen atoms and partial negative charge develops on beryllium atoms because beryllium is more electronegative than hydrogen.Due to this the bonded atoms have a dipole moment which is directed towards the hydrogen atom.
-Similarly with the other hydrogen atom the central atom has a dipole moment in the direction of the hydrogen atom.
-Dipole moment of each $Be - H$ bond is equal and opposite to each other. Therefore, they cancel out each other and the resultant dipole moment of the molecule becomes zero.
That is the reason why the \[Be{H_2}\] molecule has a zero dipole moment although the $Be - H$ Bonds are polar.
Note:
Can also solve this question using the formula of the resultant dipole moment-
$ \Rightarrow $ R=$\sqrt {{P^2} + {Q^2} + 2PQ\cos \theta } $ where P and Q are dipole moments of the polyatomic molecules.
Here the angle between the $Be - H$bond is ${180^ \circ }$ and the dipole moments between the two $Be - H$bonds are equal so we can write-
$ \Rightarrow $ R=$\sqrt {{\mu ^2} + {\mu ^2} + 2\mu \times \mu \times \cos {{180}^ \circ }} $
We know that$\cos {180^ \circ } = - 1$ so on applying this we get-
$ \Rightarrow $ R=$\sqrt {{\mu ^2} + {\mu ^2} - 2\mu \times \mu } $
Now we know that ${\left( {a - b} \right)^2} = {a^2} + {b^2} + 2ab$ so on applying this, we get-
$ \Rightarrow $ R=$\sqrt {{{\left( {\mu - \mu } \right)}^2}} $
On solving, we get-
$ \Rightarrow $ R=$0$
Hence the resultant dipole moment is zero.
Complete step by step answer:
We already know about the dipole moment. Polarity causes a molecule to have a dipole moment. There are some important points about dipole moment-
-In the case of polyatomic molecules the dipole moment not only depends upon the individual bonds but also on the spatial arrangement of various bonds in the molecule.
In such a case a molecule will have a dipole moment if the summation of all of the individual dipole moments is non-zero.
-Now, we know that in \[Be{H_2}\]molecule beryllium is the central atom which has no lone pair of electrons, only two bond pairs in its valence shell. These pairs form a covalent bond with two hydrogen atoms and the structure we obtain is linear which is given as-$H - Be - H$ .
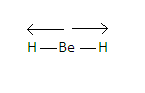
-Now we know that $Be - H$ Bond is polar as partial positive charge develops on hydrogen atoms and partial negative charge develops on beryllium atoms because beryllium is more electronegative than hydrogen.Due to this the bonded atoms have a dipole moment which is directed towards the hydrogen atom.
-Similarly with the other hydrogen atom the central atom has a dipole moment in the direction of the hydrogen atom.
-Dipole moment of each $Be - H$ bond is equal and opposite to each other. Therefore, they cancel out each other and the resultant dipole moment of the molecule becomes zero.
That is the reason why the \[Be{H_2}\] molecule has a zero dipole moment although the $Be - H$ Bonds are polar.
Note:
Can also solve this question using the formula of the resultant dipole moment-
$ \Rightarrow $ R=$\sqrt {{P^2} + {Q^2} + 2PQ\cos \theta } $ where P and Q are dipole moments of the polyatomic molecules.
Here the angle between the $Be - H$bond is ${180^ \circ }$ and the dipole moments between the two $Be - H$bonds are equal so we can write-
$ \Rightarrow $ R=$\sqrt {{\mu ^2} + {\mu ^2} + 2\mu \times \mu \times \cos {{180}^ \circ }} $
We know that$\cos {180^ \circ } = - 1$ so on applying this we get-
$ \Rightarrow $ R=$\sqrt {{\mu ^2} + {\mu ^2} - 2\mu \times \mu } $
Now we know that ${\left( {a - b} \right)^2} = {a^2} + {b^2} + 2ab$ so on applying this, we get-
$ \Rightarrow $ R=$\sqrt {{{\left( {\mu - \mu } \right)}^2}} $
On solving, we get-
$ \Rightarrow $ R=$0$
Hence the resultant dipole moment is zero.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




