
Explain the geometrical meaning of angular momentum.
Answer
516.7k+ views
Hint: The angular momentum is considered to be the rotational analogue of the linear momentum. The angular momentum of a body is defined as the cross product of the position of the body relative to the origin and the linear momentum of the body. To obtain the geometrical interpretation of the angular momentum we can represent the position vector of the body graphically as it rotates about a given axis.
Formulae used:
The angular momentum of a body is given by, $\vec L = \vec r \times \vec p$ where $\vec r$ is the position vector of the body relative to the origin and $\vec p$ is the linear momentum vector of the particle.
The linear momentum of a body is given by, $\vec p = m\vec v$ where $m$ is the mass of the body and $\vec v$ is its velocity.
Complete step by step solution:
Step 1: Sketch a graph depicting the linear momentum vector and the position vector of a particle rotating in an anticlockwise direction.
We consider a particle that rotates in the XY plane about the z-axis as shown in the figure sketched below.
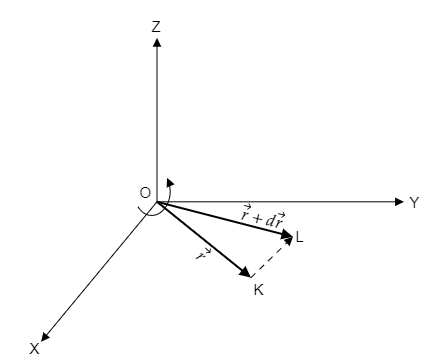
In the above figure, at any instant of time $t$ , $OK = \vec r$ represents the position vector of the particle and at a time $t + dt$ , the position vector of the particle is represented as $OL = \vec r + d\vec r$ .
As the particle rotates, the position vector of the particle will sweep an area $\left| {d\vec A} \right|$ in a small interval of time ${\text{dt}}$ .
Step 2: Express the area swept by the position vector in the small interval of time.
The displacement of the particle in the small interval of time ${\text{dt}}$ will be is obtained to be $KL = \left( {\vec r + d\vec r} \right) - \vec r = d\vec r$ .
From the above figure, the area swept by the position vector in the time ${\text{dt}}$ can be expressed as
$\left| {d\vec A} \right| = \dfrac{1}{2}\left| {OK \times KL} \right| = \dfrac{1}{2}\left| {\vec r \times d\vec r} \right|$ -------- (1)
Dividing equation (1) by ${\text{dt}}$ we get, $\left| {\dfrac{{d\vec A}}{{dt}}} \right| = \dfrac{1}{2}\left| {\vec r \times \dfrac{{d\vec r}}{{dt}}} \right|$
Now we know that the first derivative of the position vector with respect to time corresponds to the velocity vector of the particle i.e., $\dfrac{{d\vec r}}{{dt}} = \vec v$ . We also know that the linear momentum vector of the particle can be expressed as $\vec p = m\vec v \Rightarrow \vec v = \dfrac{{\vec p}}{m}$ .
So the area swept by the position vector per unit time becomes,
$\left| {\dfrac{{d\vec A}}{{dt}}} \right| = \dfrac{1}{2}\left| {\vec r \times \dfrac{{\vec p}}{m}} \right| = \dfrac{1}{{2m}}\left| {\vec r \times \vec p} \right|$ --------- (2)
The angular momentum of the particle is expressed as $\vec L = \vec r \times \vec p$-------- (3)
Substituting equation (3) in (2) we get, $\left| {\dfrac{{d\vec A}}{{dt}}} \right| = \dfrac{1}{{2m}}\left| {\vec L} \right|$
$ \Rightarrow \left| {\vec L} \right| = 2m\left| {\dfrac{{d\vec A}}{{dt}}} \right|$ ---------(4)
In equation (4), the term $\left| {\dfrac{{d\vec A}}{{dt}}} \right|$ refers to the areal velocity of the position vector of the particle.
So from equation (4), we can conclude that the angular momentum of a particle about a given axis will be twice the product of the mass of the particle and the areal velocity of the position vector of the particle. This is considered to be the geometrical interpretation of the angular momentum.
Note: Here the area swept by the position vector is given by the area of the triangle OKL whose base is the displacement vector $KL = d\vec r$ and height is the position vector $OK = \vec r$ . Since the area of a triangle is given by the formula, ${\text{Area}} = \dfrac{1}{2}\left( {{\text{height}} \times {\text{base}}} \right)$ we obtain the area swept by the position vector as given by equation (1). In equation (2), the mass of the particle is taken outside the modulus bracket because it is a scalar quantity and will always be positive.
Formulae used:
The angular momentum of a body is given by, $\vec L = \vec r \times \vec p$ where $\vec r$ is the position vector of the body relative to the origin and $\vec p$ is the linear momentum vector of the particle.
The linear momentum of a body is given by, $\vec p = m\vec v$ where $m$ is the mass of the body and $\vec v$ is its velocity.
Complete step by step solution:
Step 1: Sketch a graph depicting the linear momentum vector and the position vector of a particle rotating in an anticlockwise direction.
We consider a particle that rotates in the XY plane about the z-axis as shown in the figure sketched below.

In the above figure, at any instant of time $t$ , $OK = \vec r$ represents the position vector of the particle and at a time $t + dt$ , the position vector of the particle is represented as $OL = \vec r + d\vec r$ .
As the particle rotates, the position vector of the particle will sweep an area $\left| {d\vec A} \right|$ in a small interval of time ${\text{dt}}$ .
Step 2: Express the area swept by the position vector in the small interval of time.
The displacement of the particle in the small interval of time ${\text{dt}}$ will be is obtained to be $KL = \left( {\vec r + d\vec r} \right) - \vec r = d\vec r$ .
From the above figure, the area swept by the position vector in the time ${\text{dt}}$ can be expressed as
$\left| {d\vec A} \right| = \dfrac{1}{2}\left| {OK \times KL} \right| = \dfrac{1}{2}\left| {\vec r \times d\vec r} \right|$ -------- (1)
Dividing equation (1) by ${\text{dt}}$ we get, $\left| {\dfrac{{d\vec A}}{{dt}}} \right| = \dfrac{1}{2}\left| {\vec r \times \dfrac{{d\vec r}}{{dt}}} \right|$
Now we know that the first derivative of the position vector with respect to time corresponds to the velocity vector of the particle i.e., $\dfrac{{d\vec r}}{{dt}} = \vec v$ . We also know that the linear momentum vector of the particle can be expressed as $\vec p = m\vec v \Rightarrow \vec v = \dfrac{{\vec p}}{m}$ .
So the area swept by the position vector per unit time becomes,
$\left| {\dfrac{{d\vec A}}{{dt}}} \right| = \dfrac{1}{2}\left| {\vec r \times \dfrac{{\vec p}}{m}} \right| = \dfrac{1}{{2m}}\left| {\vec r \times \vec p} \right|$ --------- (2)
The angular momentum of the particle is expressed as $\vec L = \vec r \times \vec p$-------- (3)
Substituting equation (3) in (2) we get, $\left| {\dfrac{{d\vec A}}{{dt}}} \right| = \dfrac{1}{{2m}}\left| {\vec L} \right|$
$ \Rightarrow \left| {\vec L} \right| = 2m\left| {\dfrac{{d\vec A}}{{dt}}} \right|$ ---------(4)
In equation (4), the term $\left| {\dfrac{{d\vec A}}{{dt}}} \right|$ refers to the areal velocity of the position vector of the particle.
So from equation (4), we can conclude that the angular momentum of a particle about a given axis will be twice the product of the mass of the particle and the areal velocity of the position vector of the particle. This is considered to be the geometrical interpretation of the angular momentum.
Note: Here the area swept by the position vector is given by the area of the triangle OKL whose base is the displacement vector $KL = d\vec r$ and height is the position vector $OK = \vec r$ . Since the area of a triangle is given by the formula, ${\text{Area}} = \dfrac{1}{2}\left( {{\text{height}} \times {\text{base}}} \right)$ we obtain the area swept by the position vector as given by equation (1). In equation (2), the mass of the particle is taken outside the modulus bracket because it is a scalar quantity and will always be positive.
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

What is 1s 2s 2p 3s 3p class 11 chemistry CBSE

State the laws of reflection of light

Difference Between Prokaryotic Cells and Eukaryotic Cells




